
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
下列命题:
①若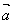 与
与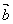 共线,则存在唯一的实数
共线,则存在唯一的实数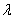 ,使
,使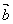 =
=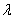
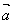 ;
;
②若向量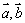 所在的直线为异面直线,则向量
所在的直线为异面直线,则向量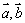 一定不共面;
一定不共面;
③向量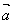 、
、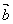 、
、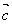 共面,则它们所在直线也共面;
共面,则它们所在直线也共面;
④若 三点不共线,
三点不共线,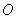 是平面ABC外一点.若
是平面ABC外一点.若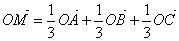 ,则点M一定在平面ABC上,且在△ABC内部,
,则点M一定在平面ABC上,且在△ABC内部,
其中正确的命题有____________(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=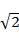 ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
(1)求直线PB与平面POC所成角的余弦值;
(2)求B点到平面PCD的距离;
(3)线段PD上是否存在一点Q,使得二面角Q-AC-D的余弦值为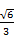 ?若存在,求出
?若存在,求出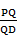 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
当x∈R,|x|< 1时,有如下表达式:
1时,有如下表达式:
1+x+x2+…+xn+…=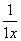 ,
,
两边同时积分得:∫ 01dx+∫
01dx+∫ 0xdx+∫
0xdx+∫ 0x2dx+…+∫
0x2dx+…+∫ 0xndx+…=∫
0xndx+…=∫ 0
0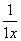 dx,
dx,
从而得到如下等式:
1× +
+ ×(
×( )2+
)2+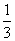 ×(
×( )3+…+
)3+…+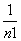 ×(
×( )n+1+…=ln2,
)n+1+…=ln2,
请根据以上材料所蕴含的数学思想方法,计算:
C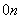 ×
× +
+ C
C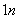 ×(
×( )2+
)2+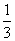 C
C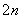 ×(
×( )3+…+
)3+…+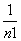 C
C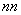 ×(
×( )n+1=________.
)n+1=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C: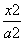 +y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:(x-3)2+(y-1)2=3相切.
+y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:(x-3)2+(y-1)2=3相切.
(1)求椭圆C的方程;
(2)若不过点A的动直线l与椭圆C交于P、Q两点,且 =0.求证:直线l过定点,并求出该定点的坐
=0.求证:直线l过定点,并求出该定点的坐 标.
标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com