
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=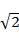 ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
(1)求直线PB与平面POC所成角的余弦值;
(2)求B点到平面PCD的距离;
(3)线段PD上是否存在一点Q,使得二面角Q-AC-D的余弦值为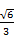 ?若存在,求出
?若存在,求出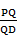 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
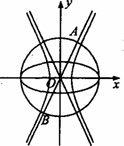
如图,已知椭圆C1: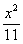 +y2=1,双曲线C2:
+y2=1,双曲线C2: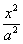 —
—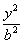 =1(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A、B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为 ( )
=1(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A、B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为 ( )
A. B.5 C.
B.5 C.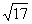 D.
D.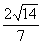
查看答案和解析>>
科目:高中数学 来源: 题型:
已知等比数列{an}的前n项和为Sn,若S2n=4(a1+a3+a5+…+a2n-1), a1a2a3=27,则a6=( )
A.27  B.81
B.81
C. 243 D.729
查看答案和解析>>
科目:高中数学 来源: 题型:
观察下列等式
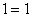 第一个式子
第一个式子
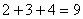 第二个式子
第二个式子
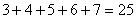 第三个式子
第三个式子
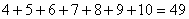 第四个式子
第四个式子
照此规律下去
(Ⅰ)写出第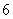 个等式;
个等式;
(Ⅱ)你能做出什么一般性的猜想?请用数学归纳法证明猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com