练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知椭圆C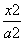：＋y2＝1(a>1)的上顶点为A，右焦点为F，直线AF与圆M：(x－3)2＋(y－1)2＝3相切．

    (1)求椭圆C的方程；

    (2)若不过点A的动直线l与椭圆C交于P、Q两点，且＝0.求证：直线l过定点，并求出该定点的坐标．


    1)椭圆的方程为＋y2＝1.

    (2)由·＝0知AP⊥AQ，从而直线AP与坐标轴不垂直，故可设直线AP的方程为y＝kx＋1，直线AQ的方程为y＝－x＋1，

    将y＝kx＋1代入椭圆C的方程，

    整理得(1＋3k2)x2＋6kx＝0，

    所以直线l过定点(0，－)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    定义方程的实数根叫做函数的“新驻点”，若函数，,的“新驻点”分别为，则的大小关系为(    )

        A.      B.      C.      D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线的参数方程是（为参数），以原点为极点，轴的正半轴为极轴建立极坐标系，圆的极坐标方程为，则直线被圆所截得的弦长等于           .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等比数列{an}的前n项和为Sn，若S2n＝4(a1＋a3＋a5＋…＋a2n－1), a1a2a3＝27，则a6＝(　　)

    A．27　 　  B．81　　 　

    C. 243　　    D．729

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     给出下列命题：

    ①已知线性回归方程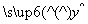＝3＋2x，当变量x增加2个单位，其预报值平均增加4个单位；

    ②在进制计算中，100(2)＝11(3)；

    ③若ξ～N(3，σ2)，且P(0≤ξ≤3)＝0.4，则P(ξ<6)＝0.1；

    ④“a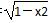＝x”是“函数y＝cos2(ax)－sin2(ax)的最小正周期为4”的充要条件；

    ⑤设函数f(x)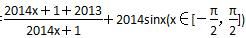＝的最大值为M，最小值为m，则M＋m＝4027，其中正确命题的个数是________个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知是等差数列的前n项和，若， 则等于（   ）

    A. 18          B. 36           C 72        D无法确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    两个三口之家，共4个大人，2个小孩，约定星期日乘“奥迪”、“捷达”两

    辆轿车结伴郊游，每辆车最多只能乘坐4人，其中两个小孩不能独坐一辆车，则不同的乘车方法种数是（   ）

     A. 40         B. 48          C. 60          D. 68

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    曲线f(x)=x3－2x+1在点(1, 0)处的切线方程为（   ）

    A．y=－x+1        B．y=x－1             C．y=2x－2        D．y=－2x+2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    cos390°=（　　）

    　

    A．

    B．

    C．

    D．

    ﹣

    查看答案和解析>>

    同步练习册答案