练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知集合A＝{x|x2－2x－3≤0，x∈R}，B＝{x|x2－2mx＋m2－4≤0，x∈R，m∈R}．

    (1)若A∩B＝[0,3]，求实数m的值；

    (2)若A⊆∁RB，求实数m的取值范围．


    解：由已知得：A＝{x|－1≤x≤3}，B＝{x|m－2≤x≤m＋2}．

    (1)∵A∩B＝[0,3]，

    ∴                        ∴∴m＝2.

    (2)∁RB＝{x|x＜m－2或x＞m＋2}．

    ∵A⊆∁RB，∴m－2＞3，或m＋2＜－1，

                                      ∴m＞5或m＜－3.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知等比数列{an}为递增数列，且a＝a10,2(an＋an＋2)＝5an＋1，则数列{an}的通项公式an＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在某运动会期间，为使观众提前知道票价，票务网站公布球类比赛的门票价格如下表，某球迷赛前准备了1200元预订15张下表中球类比赛的门票.

    比赛项目

    票价(元/场)

    足球

    篮球

    乒乓球

    100

    80

    60

    若在准备资金允许的范围内和总票数不变的前提下，该球迷想预订上表中三种球类比赛门票，其中篮球比赛门票数与乒乓球比赛门票数相同，且篮球比赛门票的费用不超过足球比赛门票的费用，求可以预订的足球比赛门票数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若正数x，y满足x＋3y＝5xy，则3x＋4y的最小值是(　　)

    A.                              B.

    C．5                               D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知不等式ax2－bx－1≥0的解集是，则不等式x2－bx－a＜0的解集是(　　)

    A．(2,3)                          B．(－∞，2)∪(3，＋∞)

    C.                         D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    不等式ax2－bx＋c＞0的解集是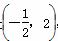，对于系数a，b，c有下列结论：

    ①a＞0；②b＞0；③c＞0；④a＋b＋c＞0；⑤a－b＋c＞0.

    其中正确结论的序号是________(把你认为正确结论的序号都填上)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    由不等式组所确定的平面区域的面积为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等式：sin25°＋cos235°＋sin5°cos35°＝；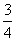

    sin215°＋cos245°＋sin15°cos45°＝；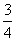

    sin230°＋cos260°＋sin30°cos60°＝；….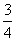

    由此可归纳出对任意角θ都成立的一个等式，并予以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列结论正确的是(　　)

    A．各个面都是三角形的几何体是三棱锥

    B．以正方形的一条对角线为轴旋转一周围成的几何体叫圆锥

    C．棱锥的侧棱长与底面多边形的边长都相等，则此棱锥可能是正六棱锥

    D．圆锥的顶点与底面圆周上的任意一点的连线都是母线

    查看答案和解析>>

    同步练习册答案