
已知等式:sin25°+cos235°+sin5°cos35°=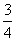 ;
;
sin215°+cos245°+sin15°cos45°=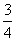 ;
;
sin230°+cos260°+sin30°cos60°=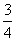 ;….
;….
由此可归纳出对任意角θ都成立的一个等式,并予以证明.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m 的值;
的值;
(2)若A⊆∁RB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
对任意正整数a,b,a+b≥2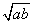 大前提
大前提
x+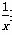 ≥2
≥2 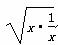 小前提
小前提
所以x+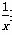 ≥2结论
≥2结论
以上推理过程中的错误为( )
A.大前提 B.小前提
C.结论 D.无错误
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)= (x>0),观察:
(x>0),观察:
f1(x)=f(x)= ,
,
f2(x)=f(f1(x))=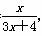 ,
,
f3(x)=f(f2(x))=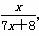 ,
,
f4(x)=f(f3(x))=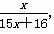 ,
,
…
根据以上事实,由归纳推理可得:
当n∈N*且n≥2时,fn(x)=f(fn-1(x))=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
以下几个命题中,正确命题的个数是( )
①不共面的四点中,其中任意三点不共线;
②若点A、B、C、D共面,点A、B、C、E共面,则A、B、C、D、E共面;
③若直线a、b共面,直线a、c共面,则直线b、c共面;
④依次首尾相接的四条线段必共面.
A.0 B.1
C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com