练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    以下几个命题中，正确命题的个数是(　　)

    ①不共面的四点中，其中任意三点不共线；

    ②若点A、B、C、D共面，点A、B、C、E共面，则A、B、C、D、E共面；

    ③若直线a、b共面，直线a、c共面，则直线b、c共面；

    ④依次首尾相接的四条线段必共面．

    A．0　　　　　　　　　　          B．1

    C．2                              D．3


    B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知等式：sin25°＋cos235°＋sin5°cos35°＝；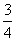

    sin215°＋cos245°＋sin15°cos45°＝；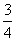

    sin230°＋cos260°＋sin30°cos60°＝；….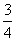

    由此可归纳出对任意角θ都成立的一个等式，并予以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列结论正确的是(　　)

    A．各个面都是三角形的几何体是三棱锥

    B．以正方形的一条对角线为轴旋转一周围成的几何体叫圆锥

    C．棱锥的侧棱长与底面多边形的边长都相等，则此棱锥可能是正六棱锥

    D．圆锥的顶点与底面圆周上的任意一点的连线都是母线

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，已知正方体ABCD－A1B1C1D1的棱长为2，O为底面正方形ABCD的中心，则三棱锥B1－BCO的体积为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知一个圆柱的底面直径与高均为2R，一个圆锥的底面直径与高均为2r，若圆柱的表面积与圆锥的表面积相等，则R2∶r2＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，正方体ABCD－A1B1C1D1中，E、F分别是AB和AA1的中点．求证：

    (1)E、C、D1、F四点共面；

    (2)CE、D1F、DA三线共点．

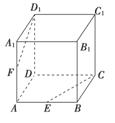
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线l∥平面α，P∈α，那么过点P且平行于直线l的直线(　　)

    A．只有一条，不在平面α内                         

    B．有无数条，不一定在平面α内

    C．只有一条，且在平面α内

    D．有无数条，一定在平面α内

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知α，β是两个不同的平面，m，n是两条不重合的直线，则下列命题中正确的是(　　)

    A．若m∥α，α∩β＝n，则m∥n

    B．若m⊥α，m⊥n，则n∥α

    C．若m⊥α，n⊥β，α⊥β，则m⊥n

    D．若α⊥β，α∩β＝n，m⊥n，则m⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点E、F分别在正方体ABCD­A1B1C1D1的棱BB1、CC1上，且B1E＝2EB，CF＝2FC1，则面AEF与面ABC所成的二面角的正切值等于________．

    查看答案和解析>>

    同步练习册答案