练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

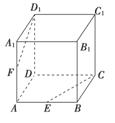
    如图，正方体ABCD－A1B1C1D1中，E、F分别是AB和AA1的中点．求证：

    (1)E、C、D1、F四点共面；

    (2)CE、D1F、DA三线共点．


    证明：(1)如图，连接EF，CD1，A1B.

    ∵E、F分别是AB、AA1的中点，

    ∴EF∥BA1.

    又A1B∥D1C，

    ∴EF∥CD1，

    ∴E、C、D1、F四点共面．

    (2)∵EF∥CD1，EF＜CD1，

    ∴CE与D1F必相交，设交点为P，则由P∈CE，CE⊂平面ABCD，

    得P∈平面ABCD.

    同理P∈平面ADD1A1.

    又平面ABCD∩平面ADD1A1＝DA.

    ∴P∈直线DA，∴CE、D1F、DA三线共点．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设函数f(x)＝ (x>0)，观察：

    f1(x)＝f(x)＝，

    f2(x)＝f(f1(x))＝，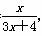

    f3(x)＝f(f2(x))＝，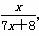

    f4(x)＝f(f3(x))＝，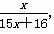

    …

    根据以上事实，由归纳推理可得：

    当n∈N*且n≥2时，fn(x)＝f(fn－1(x))＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个正方体内接于高为40 cm，底面半径为30 cm的圆锥中，求正方体的棱长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正四棱锥S－ABCD中，SA＝2，那么当该棱锥的体积最大时，它的高为(　　)

    A．1　　　　　　　　　　          B.

    C．2                              D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    以下几个命题中，正确命题的个数是(　　)

    ①不共面的四点中，其中任意三点不共线；

    ②若点A、B、C、D共面，点A、B、C、E共面，则A、B、C、D、E共面；

    ③若直线a、b共面，直线a、c共面，则直线b、c共面；

    ④依次首尾相接的四条线段必共面．

    A．0　　　　　　　　　　          B．1

    C．2                              D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在正方体ABCD－A1B1C1D1中，E、F分别为棱AA1、CC1的中点，则在空间中与三条直线A1D1、EF、CD都相交的直线有________条．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在空间四边形ABCD中，M∈AB，N∈AD，若＝，则直线MN与平面BDC的位置关系是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，在四棱锥P－ABCD中，PA⊥底面ABCD，且底面各边都相等，M是PC上的一动点，当点M满足__________时，平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)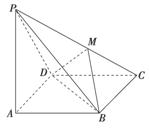

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某单位有职工100人，不到35岁的有45人，35岁到49岁的有25人，剩下的为50岁以上的人，用分层抽样法从中抽取20人，各年龄段分别抽取的人数为(　　)

    A．7,5,8                          B．9,5,6

    C．6,5,9                          D．8,5,7

    查看答案和解析>>

    同步练习册答案