练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若的值为             .


     -1/3


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知等比数列的公比为正数，且.  

    （1）求的通项公式；

    （2）设是首项为1，公差为2的等差数列，求数列的前项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    抛物线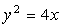上有两个定点A、B分别在对称轴的上、下两侧，F为抛物线的焦点，并且|FA|=2，|FB|=5，在抛物线AOB这段曲线上求一点P，使△PAB的面积最大，并求这个最大面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数是R上的偶函数，其图像关于点对称，且在区间上是单调函数，求的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    复数的虚部为____________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正方体棱长1，顶点A、B、C、D在半球的底面内，顶点A1、B1、C1、D1在半球球面上，则此半球的体积是         . 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


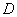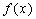    如右图（1）所示，定义在区间上的函数，如果满

    足：对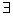，常数A，都有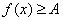成立，则称函数

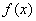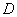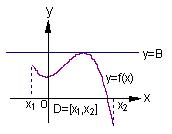
    在区间上有下界，其中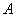称为函数的下界. （提示：图(1)、

    （2）中的常数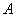、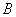可以是正数，也可以是负数或零）

    （

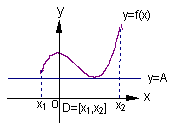    Ⅰ）试判断函数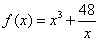在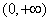上是否有下界？并说明理由；

    （Ⅱ）又如具有右图（2）特征的函数称为在区间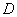上有上界.

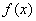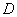    请你类比函数有下界的定义，给出函数在区间上

    有上界的定义，并判断（Ⅰ）中的函数在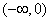上是否

    有上界？并说明理由；

    （Ⅲ）若函数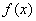在区间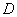上既有上界又有下界，则称函数

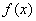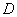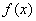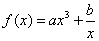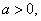
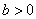
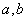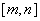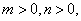
    在区间上有界，函数叫做有界函数．试探究函数 （是常数）是否是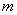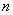（、是常数）上的有

    界函数？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知均在椭圆上，直线、分别过椭圆的左右焦点、，当时，有.

       （I）求椭圆的方程;

       （II）设P是椭圆上的任一点，为圆的任一条直径，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设为实数，是方程的两个实根，数列满足，，（…）．

    （1）证明：，；

    （2）求数列的通项公式；

    （3）若，，求的前项和．

    查看答案和解析>>

    同步练习册答案