练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数y=sin（2x+φ）（0≤φ≤π）是R上的偶函数，则φ的值是　


    　．

    考点： 由y=Asin（ωx+φ）的部分图象确定其解析式．

    专题： 计算题．

    分析： 根据函数y=sin（2x+φ）的图象特征，若它是偶函数，只需要x=0时，函数能取得最值．

    解答： 解：函数y=sin（2x+ϕ）是R上的偶函数，就是x=0时函数取得最值，

    所以f（0）=±1

    即sinϕ=±1

    所以ϕ=kπ+（k∈Z），

    当且仅当取 k=0时，得φ=，符合0≤φ≤π

    故答案为：


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    等差数列中，已知，试求n的值        

    查看答案和解析>>

    科目：高中数学 来源： 题型：


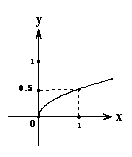
    某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元（如图）

    （3）       分别写出两种产品的收益与投资的函数关系；

    （4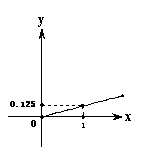）       该家庭现有20万元资金，全部用于理财投资，问：怎样分配资金能使投资获得最大收益，其最大收益为多少万元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某“农家乐”接待中心有客房200间，每间日租金为40元，每天都客满．根据实际需要，该中心需提高租金．如果每间客房日租金每增加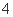元，客房出租就会减少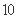间．（不考虑其他因素）

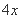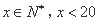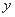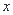    （1）设每间客房日租金提高元（），记该中心客房的日租金总收入为，试用表示；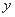

    （2）在（1）的条件下，每间客房日租金为多少时，该中心客房的日租金总收入最高？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    二项式（x+1）10展开式中，x8的系数为　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数y=xa+b，x∈（0，+∞）是增函数，则（　　）

    　 A． a＞0，b是任意实数 B． a＜0，b是任意实数 C． b＞0，a是任意实数 D． b＜0，a是任意实数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    “tanx=﹣1”是“x=﹣+2kπ（k∈Z）”的（　　）

    　     A． 充分非必要条件 B． 必要非充分条件　 C． 充要条件 D． 既非充分又非必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知全集为R，集合，则集合

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一次二期课改经验交流会打算交流试点学校的论文5篇和非试点学校的论文3篇. 若任

       意排列交流次序，则最先和最后交流的论文都为试点学校的概率是__          (结果用分数表示).

    查看答案和解析>>

    同步练习册答案