
某“农家乐”接待中心有客房200间,每间日租金为40元,每天都客满.根据实际需要,该中心需提高租金.如果每间客房日租金每增加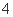 元,客房出租就会减少
元,客房出租就会减少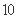 间.(不考虑其他因素)
间.(不考虑其他因素)
(1)设每间客房日租金提高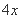 元(
元(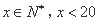 ),记该中心客房的日租金总收入为
),记该中心客房的日租金总收入为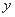 ,试用
,试用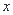 表示
表示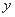 ;
;
(2)在(1)的条件下,每间客房日租金为多少时,该中心客房的日租金总收入最高?
科目:高中数学 来源: 题型:
椭圆C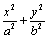 =1(
=1(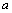 >
>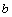 >0)的离心率
>0)的离心率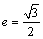 ,
,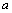 +
+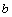 =3.
=3.
(Ⅰ)求椭圆C的方程;
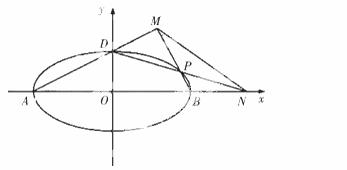
(Ⅱ)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意点,直线DP交x轴于点N直线AD交BP于点M,设BP的斜率为k,MN的斜率为m,证明2m-k为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
“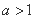 ”是“
”是“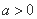 ” 的………………………………………………………………( )
” 的………………………………………………………………( )
(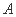 )充分非必要条件 (
)充分非必要条件 (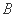 )必要非充分条件
)必要非充分条件
(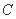 )充要条件 (
)充要条件 (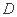 )既非充分又非必要条件
)既非充分又非必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
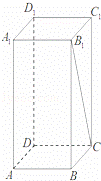
如图,正四棱柱ABCD﹣A1B1C1D1的底面边长AB=2,若异面直线A1A与B1C所成角的大小为arctan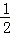 ,求正四棱柱ABCD﹣A1B1C1D1的体积.
,求正四棱柱ABCD﹣A1B1C1D1的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com