练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一次猜奖游戏中，1，2，3，4四扇门里摆放了， ， ， 四件奖品（每扇门里仅放一件）.甲同学说：1号门里是，3号门里是；乙同学说：2号门里是，3号门里是；丙同学说：4号门里是，2号门里是；丁同学说：4号门里是，3号门里是.如果他们每人都猜对了一半，那么4号门里是（ ）

    A. B. C. D.

    【答案】A

    【解析】 由题意得，甲同学说：1号门里是，3号门里是，乙同学说：2号门里是，3号门里是；丙同学说：4号门里是，2号门里是；丁同学说：4号门里是，3号门里是 ，若他们每人猜对了一半，则可判断甲同学中1号门中是是正确的；乙同学说的2号门中有是正确的；并同学说的3号门中有是正确的；丁同学说的4号门中有是正确的，则可判断在四扇门中，分别存有 ，所以号门里是，故选A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】三个臭皮匠顶上一个诸葛亮，能顶得上吗？在一次有关“三国演义”的知识竞赛中，三个臭皮匠A、B、C能答对题目的概率分别为P(A)＝，P(B)＝，P(C)＝，诸葛亮D能答对题目的概率为P(D)＝，如果将三个臭皮匠A、B、C组成一组与诸葛亮D比赛，答对题目多者为胜方，问哪方胜？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (1)求时，求的单调区间；

    (2)讨论在定义域上的零点个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

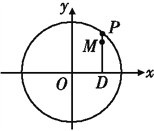
    【题目】如图,设P是圆上的动点,点D是P在x轴上的投影，M为线段PD上一点,且，

    (1)当P在圆上运动时,求点M的轨迹C的方程；

    (2)求过点(3,0)且斜率为的直线被轨迹C所截线段的长度.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校为了纪念“中国红军长征90周年”，增强学生对“长征精神”的深刻理解，在全校组织了一次有关“长征”的知识竞赛，经过初赛、复赛，甲、乙两个代表队(每队3人)进入了决赛，规定每人回答一个问题，答对为本队赢得20分，答错得0分.假设甲队中每人答对的概率均为，乙队中3人答对的概率分别为， ， ，且各人回答正确与否相互之间没有影响，用表示乙队的总得分.

    (1)求的分布列和均值；

    (2)求甲、乙两队总得分之和等于40分且甲队获胜的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求曲线在点处的切线方程；

    （2）求函数的极值；

    （3）判断在上的单调性，并加以说明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（）.

    （1）讨论函数极值点的个数，并说明理由；

    （2）若， 恒成立，求的最大整数值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂需要确定加工某大型零件所花费的时间，连续4天做了4次统计，得到的数据如下：

    零件的个数（个）

    2

    3

    4

    5

    加工的时间（小时）

    2.5

    3

    4

    5.5

    （1）在直角坐标系中画出以上数据的散点图，求出关于的回归方程，并在坐标系中画出回归直线；

    （2）试预测加工10个零件需要多少时间？

    参考公式：两个具有线性关系的变量的一组数据：，

    其回归方程为，其中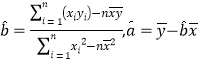

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知中心在原点，焦点在轴上的椭圆，离心率，且椭圆过点.

    (1)求椭圆的方程；

    (2)设椭圆左、右焦点分别为，过的直线与椭圆交于不同的两点，则的内切圆的面积是否存在最大值？若存在，求出这个最大值及此时的直线方程；若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案