
设△ 的三边长分别为
的三边长分别为 △
△ 的面积为
的面积为 ,内切圆半径为
,内切圆半径为 ,则
,则 .类比这个结论可知:四面体
.类比这个结论可知:四面体 的四个面的面积分别为
的四个面的面积分别为


 内切球的半径为
内切球的半径为 ,四面体
,四面体 的体积为
的体积为 ,则
,则 =( )
=( )
A.
B.
C.
D.
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源:2015-2016学年江苏省泰州市姜堰区高一上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分16分)姜堰某化学试剂厂以x千克/小时的速度匀速生产某种产品(生产条件要求 ),每小时可获得的利润是
),每小时可获得的利润是 千元.
千元.
(1)要使生产该产品2小时获得利润不低于30千元,求 的取值范围;
的取值范围;
(2)要使生产120千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求此最大利润.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年福建厦门双十中学高二上期中理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知实数 ,设函数
,设函数 .
.
(Ⅰ)证明:f(x)≥2;
(Ⅱ)若 ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016届江西省高三上学期期中文科数学试卷(解析版) 题型:解答题
已知函数 ,若存在
,若存在 使得函数
使得函数 的值域为
的值域为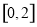 ,则实数
,则实数 的取值范围是 .
的取值范围是 .
【答案】
【解析】因为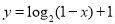 在
在 上是减函数,所以
上是减函数,所以 ,由函数
,由函数 为值域知
为值域知 ,解得
,解得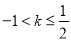 .令
.令 ,则
,则 =
= ,知
,知 在
在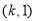 上为减函数,在
上为减函数,在 为增函数.又由
为增函数.又由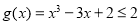 ,得
,得 ,且
,且 ,则必有
,则必有 .如图所示.易知
.如图所示.易知 .
.

试题分析:
考点:1、函数的定义域与值域;2、函数的单调性;3、函数图象的应用;4、分段函数.
【易错点晴】本题解答如果不能正确作出函数的图象就无法利用数形结合法直观求解,同时如果确定出函数图象后,不能正确求得切线 的取值范围也不能得到正确的结果,因此解答本题的关键是求出
的取值范围也不能得到正确的结果,因此解答本题的关键是求出 的范围,不然会误认为
的范围,不然会误认为 .
.
【题型】填空题
【适用】较易
【标题】【百强校】2016届江西省临川一中高三上学期期中文科数学试卷(带解析)
【关键字标签】
【结束】
(本小题满分10分)已知集合 .
.
(1)若 ,求出实数
,求出实数 的值;
的值;
(2)若命题 命题
命题 且
且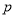 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com