
| A. | 在区间[$\frac{π}{2}$,$\frac{3π}{2}$]上单调递减 | B. | 在区间[0,$\frac{3π}{2}$]上单调增 | ||
| C. | 在区间[0,π]上单调递减 | D. | 在区间[0,π]上单调增 |
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
| 原料 种类 | 磷酸盐(单位:吨) | 硝酸盐(单位:吨) |
| 甲 | 4 | 20 |
| 乙 | 2 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工程队在南海海域进行填海造地工程,欲在边长为1千米的正三角形岛礁ABC的外围选择一点D(D在平面ABC内),建设一条军用飞机跑道AD,在点D测得B、C两点的视角∠BDC=60°,如图所示,记∠CBD=θ,如何设计θ,使得飞机跑道AD最长?
某工程队在南海海域进行填海造地工程,欲在边长为1千米的正三角形岛礁ABC的外围选择一点D(D在平面ABC内),建设一条军用飞机跑道AD,在点D测得B、C两点的视角∠BDC=60°,如图所示,记∠CBD=θ,如何设计θ,使得飞机跑道AD最长?查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
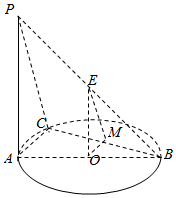 如图所示,AB为⊙O的直径,点C在⊙O上,PA⊥平面ABC,点E为线段PB的中点,点M为BC的中点.
如图所示,AB为⊙O的直径,点C在⊙O上,PA⊥平面ABC,点E为线段PB的中点,点M为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
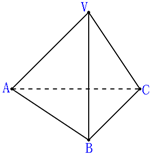 如图,三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2$\sqrt{3}$,VC=1则二面角V-AB-C的平面角的度数为( )
如图,三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2$\sqrt{3}$,VC=1则二面角V-AB-C的平面角的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com