
| ԭ�� ���� | �����Σ���λ���֣� | �����Σ���λ���֣� |
| �� | 4 | 20 |
| �� | 2 | 20 |
���� ����������ɵ�4x+2y��8��20x+20y��60����x��y��0������ֱ�ߵĻ�������϶�Ԫһ�β���ʽ�������ɵõ���
�������������ַ���x��Ƥ�����ַ���y��Ƥ���ܹ���������z��Ԫ����Ŀ�꺯��Ϊz=3x+2y����z=3x+2y����Ϊ$y=-\frac{3}{2}x+\frac{1}{2}z$���ɵ�z�ļ�������Ϊy���ϵĽؾ��2��������ƽ�Ʒ������ɵõ��������ֵ��
��� 
 �⣺���������⣬x��y�������ѧ��ϵʽΪ��
�⣺���������⣬x��y�������ѧ��ϵʽΪ��
$\left\{\begin{array}{l}4x+2y��8\\ 20x+20y��60\\ x��0\\ y��0\end{array}\right.$��$\left\{\begin{array}{l}2x+y��4\\ x+y��3\\ x��0\\ y��0\end{array}\right.$��
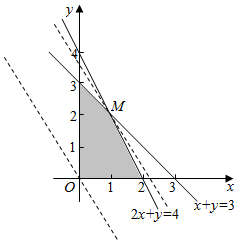
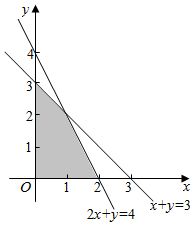
��ֱ������ϵ�пɱ�ʾ����ͼ��ʾ��ƽ��������Ӱ���֣���
�������������ַ���x��Ƥ�����ַ���y��Ƥ��
�ܹ���������z��Ԫ����Ŀ�꺯��Ϊz=3x+2y��
��������ͼ��ʾ��
��z=3x+2y����Ϊ$y=-\frac{3}{2}x+\frac{1}{2}z$��
��ͼ��֪��ֱ��$y=-\frac{3}{2}x+\frac{1}{2}z$�����������ϵĵ�Mʱ���ؾ�$\frac{1}{2}z$���
�ⷽ����$\left\{\begin{array}{l}2x+y=4\\ x+y=3\end{array}\right.$��
��ĵ�M������Ϊ��x=1��y=2�� ��
����zmax=3x+2y=3��1+2��2=7��
���������ַ���1��Ƥ�����ַ���2��Ƥ��
�ܹ���������������������7��Ԫ��
���� ���⿼�����Թ滮��ʵ����������ã�����Ŀ�꺯��������Լ�������µ���ֵ��ע���������ν�ϵ�˼�뷽��������������������ͼ�����������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{1+\sqrt{5}}}{2}$ | B�� | $\frac{{1-\sqrt{5}}}{2}$ | C�� | $\frac{{-1+\sqrt{5}}}{2}$��$\frac{{-1-\sqrt{5}}}{2}$ | D�� | $\frac{{1+\sqrt{5}}}{2}$��$\frac{{1-\sqrt{5}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 15 | B�� | 16 | C�� | 31 | D�� | 32 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 720�� | B�� | 1440�� | C�� | 1800�� | D�� | 3600�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������[$\frac{��}{2}$��$\frac{3��}{2}$]�ϵ����ݼ� | B�� | ������[0��$\frac{3��}{2}$]�ϵ����� | ||
| C�� | ������[0����]�ϵ����ݼ� | D�� | ������[0����]�ϵ����� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com