解:(1)由题中表格给出的信息可知,
函数f(x)的周期为T=

-(-

)=π,且ω>0,
∴ω=
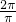
=2,
由表格得:sin[2×(-

)+φ]=0,可得:φ=

+2kπ(k∈Z),
由0<φ<π,所以φ=

,
所以函数的解析式为f(x)=sin(2x+

)=cos2x;…(6分)
(2)∵f(A)=cos2A=-

,且A为锐角,
∴2A=

,即A=

,
在△ABC中,AC=2,BC=3,
由正弦定理得
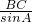
=
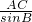
,
∴sinB=
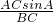
=

,
∵BC>AC,∴B<A=

,∴cosB=

,
∴sinC=sin(A+B)=sinAcosB+cosAsinB=

×

+

×

=
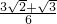
,
又AC=2,BC=3,
∴S△ABC=

AC•BC•sinC=
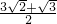
.…(12分)
分析:(1)观察表格可得出函数f(x)的周期为π,根据周期公式及ω大于0,可得出ω的值,然后再将x=-

时,y=0代入函数解析式中,并根据φ的范围,利用正弦函数的图象与性质得出φ的度数,将ω及φ的值代入,即可确定出函数f(x)的解析式;
(2)由第一问确定出的函数解析式,以及f(A)=-

,根据A为锐角,利用特殊角的三角函数值求出A的度数,进而确定出sinA及cosA的值,由sinA,AC及C的值,利用正弦定理求出sinB的值,由BC大于AC,根据大边对大角可得出B小于A,得到B的范围,由sinB的值,利用同角三角函数间的基本关系求出cosB的值,然后利用诱导公式得到sinC=sin(A+B),将sin(A+B)利用两角和与差的正弦函数公式化简后,将各自的值代入求出sin(A+B)的值,即为sinC的值,最后由AC,BC及sinC的值,利用三角形的面积公式即可求出三角形ABC的面积.
点评:此题属于解三角形的题型,涉及的知识有:三角函数的周期公式,正弦定理,两角和与差的正弦函数公式,诱导公式,以及三角形的面积公式,熟练掌握公式及定理是解本题的关键.







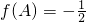 (A为锐角),求△ABC的面积.
(A为锐角),求△ABC的面积.  -(-
-(- )=π,且ω>0,
)=π,且ω>0,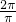 =2,
=2, )+φ]=0,可得:φ=
)+φ]=0,可得:φ= +2kπ(k∈Z),
+2kπ(k∈Z), ,
, )=cos2x;…(6分)
)=cos2x;…(6分) ,且A为锐角,
,且A为锐角, ,即A=
,即A= ,
,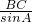 =
=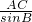 ,
,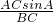 =
= ,
, ,∴cosB=
,∴cosB= ,
, ×
× +
+ ×
× =
=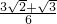 ,
, AC•BC•sinC=
AC•BC•sinC=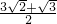 .…(12分)
.…(12分) 时,y=0代入函数解析式中,并根据φ的范围,利用正弦函数的图象与性质得出φ的度数,将ω及φ的值代入,即可确定出函数f(x)的解析式;
时,y=0代入函数解析式中,并根据φ的范围,利用正弦函数的图象与性质得出φ的度数,将ω及φ的值代入,即可确定出函数f(x)的解析式; ,根据A为锐角,利用特殊角的三角函数值求出A的度数,进而确定出sinA及cosA的值,由sinA,AC及C的值,利用正弦定理求出sinB的值,由BC大于AC,根据大边对大角可得出B小于A,得到B的范围,由sinB的值,利用同角三角函数间的基本关系求出cosB的值,然后利用诱导公式得到sinC=sin(A+B),将sin(A+B)利用两角和与差的正弦函数公式化简后,将各自的值代入求出sin(A+B)的值,即为sinC的值,最后由AC,BC及sinC的值,利用三角形的面积公式即可求出三角形ABC的面积.
,根据A为锐角,利用特殊角的三角函数值求出A的度数,进而确定出sinA及cosA的值,由sinA,AC及C的值,利用正弦定理求出sinB的值,由BC大于AC,根据大边对大角可得出B小于A,得到B的范围,由sinB的值,利用同角三角函数间的基本关系求出cosB的值,然后利用诱导公式得到sinC=sin(A+B),将sin(A+B)利用两角和与差的正弦函数公式化简后,将各自的值代入求出sin(A+B)的值,即为sinC的值,最后由AC,BC及sinC的值,利用三角形的面积公式即可求出三角形ABC的面积.

