解:(1)a
2=2S
1+1=3=3a
1,
当n≥2时,a
n+1-a
n=(2S
n+1)-(2S
n-1+1)=2a
n,(3分)
∴a
n+1=3a
n,即
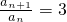
,
∴数列{a
n}是首项a
1=1,公比为3的等比数列,(4分)
从而得:
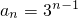
;(6分)
(2)设数列{b
n}的公差为d(d>0),
∵T
3=15,∴b
2=5,
依题意a
1+b
1,a
2+b
2,a
3+b
3成等比数列,
则有
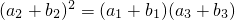
,
又a
2=3,b
1=b
2+d=5-d,b
3=b
2+d=5+d,
∴64=(5-d+1)(5+d+9),
解得:d=2或d=-10(舍去),(8分)
∵b
1=5-d=5-2=3,
∴
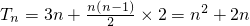
,(10分)
∵
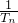
=

(

-

),
则
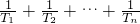
=

=

.(13分)
分析:(1)把n=1代入a
n+1=2S
n+1,并根据S
1=a
1进行化简得到a
2=3a
1,当n大于等于2时,表示出a
n+1-a
n,根据S
n-S
n-1=a
n变形,可得出a
n+1=3a
n,进而确定出数列{a
n}是首项a
1=1,公比为3的等比数列,表示出此等比数列的通项公式即可;
(2)设出等差数列{b
n}的公差为d,由已知b
1+b
2+b
3=15,利用等差数列的性质化简,可得出b
2的值,再由a
1+b
1,a
2+b
2,a
3+b
3成等比数列,利用等比数列的性质列出关系式,利用等比数列的通项公式化简得到关于d的方程,求出方程的解得到d的值,进而求出b
1的值,利用等差数列的求和公式表示出T
n,利用拆项法得到
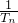
=

(

-

),
列举出T
n的各项,抵消合并后即可得到所求式子的值.
点评:此题考查了等差、等比数列的性质,等差、等比数列的通项公式,等比数列的确定,以及数列的求和,利用了拆项的方法,熟练掌握性质及公式是解本题的关键.

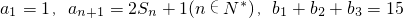
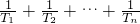 .
.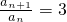 ,
,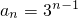 ;(6分)
;(6分)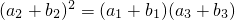 ,
,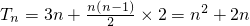 ,(10分)
,(10分)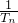 =
= (
( -
- ),
),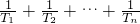

 .(13分)
.(13分)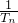 =
= (
( -
- ),
),

 名校课堂系列答案
名校课堂系列答案