
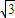 CD,求∠CAB的大小.
CD,求∠CAB的大小.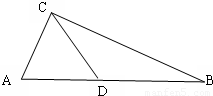
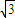 CD,利用正弦定理列出关系式,利用诱导公式变形后,将第一问得出的α+β=
CD,利用正弦定理列出关系式,利用诱导公式变形后,将第一问得出的α+β=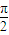 -β,α=
-β,α=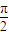 -2β代入,利用诱导公式化简,再利用二倍角的余弦函数公式化为关于cosβ的方程,求出方程的解得到cosβ的值,由α和β都为直角三角形的锐角,利用特殊角的三角函数值求出β的度数,即可得到∠CAB的度数.
-2β代入,利用诱导公式化简,再利用二倍角的余弦函数公式化为关于cosβ的方程,求出方程的解得到cosβ的值,由α和β都为直角三角形的锐角,利用特殊角的三角函数值求出β的度数,即可得到∠CAB的度数.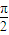 -α,∠ACD=
-α,∠ACD=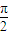 -β,
-β,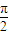 -β,即α=
-β,即α=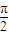 -2β,
-2β, -2β)+1-cos2β=cos2β+1-cos2β=1;
-2β)+1-cos2β=cos2β+1-cos2β=1;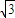 CD及正弦定理知:
CD及正弦定理知: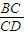 =
=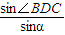 =
=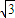 ,
,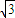 sinα,
sinα,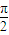 ,即α+β=
,即α+β=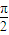 -β,α=
-β,α=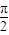 -2β,
-2β,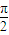 -β)=
-β)=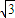 sin(
sin(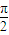 -2β),即cosβ=
-2β),即cosβ= cos2β=
cos2β=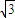 (2cos2β-1),
(2cos2β-1),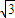 cos2β-cosβ-
cos2β-cosβ-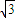 =0,
=0, 或cosβ=-
或cosβ=-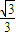 (舍去),
(舍去),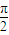 ),
),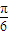 ,
,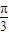 .
.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.查看答案和解析>>
科目:高中数学 来源: 题型:
 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
| ||
| 2 |
| DM |
| DN |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com