
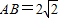 ,BC=1,以AB的中点O为原点建立如图所示的平面直角坐标系.
,BC=1,以AB的中点O为原点建立如图所示的平面直角坐标系.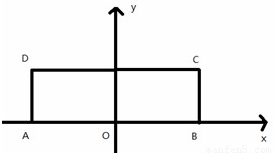
 ,得(2k2+1)x2+8kx+4=0,直线m与椭圆只有一个公共点,利用韦达定理能求出直线m的方程.
,得(2k2+1)x2+8kx+4=0,直线m与椭圆只有一个公共点,利用韦达定理能求出直线m的方程. ⊥
⊥ ,得知x1x2+y1y2=0,根据x1x2求得y1y2代入即可求得k,最后检验看是否符合题意.
,得知x1x2+y1y2=0,根据x1x2求得y1y2代入即可求得k,最后检验看是否符合题意. ,0),(
,0),( ,0),(
,0),( ,1).
,1). =1(a>b>0).
=1(a>b>0). +1=4>2
+1=4>2 ,所以a=2.
,所以a=2. +
+ =1.
=1. ,得(2k2+1)x2+8kx+4=0,
,得(2k2+1)x2+8kx+4=0, .
. x,或y=-
x,或y=- x.
x. ,得(1+2k2)x2+8kx+4=0.
,得(1+2k2)x2+8kx+4=0. ,x1x2=
,x1x2= ,
, ⊥
⊥ ,
, -
- +4=0,即
+4=0,即 =0,
=0, .
. x+2,或y=-
x+2,或y=- x+2.
x+2. x+2,或y=-
x+2,或y=- x+2.
x+2.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
 已知长方形ABCD,AB=6,BC=7/4.以AB的中点0为原点建立如图所示的平面直角坐标系x0y
已知长方形ABCD,AB=6,BC=7/4.以AB的中点0为原点建立如图所示的平面直角坐标系x0y| |0P| | |0M| |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、25π | B、50π | C、5π | D、10π |
查看答案和解析>>
科目:高中数学 来源: 题型:
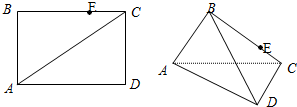
 如图,把长、宽分别为4、3的长方形ABCD沿对角线AC折成直二面角.
如图,把长、宽分别为4、3的长方形ABCD沿对角线AC折成直二面角.| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com