
 某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.如图表是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.
某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.如图表是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.| 时间分组 | 频数 |
| [0,20) | 12 |
| [20,40) | 20 |
| [40,60) | 24 |
| [60,80) | 26 |
| [80,100) | 14 |
| [100,120) | 4 |
| 非手机迷 | 手机迷 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
分析 (1)将频率视为概率,即可得出结论.
(2)利用频率分布直方图直接完成2×2列联表,通过计算K2,说明有90%的把握认为“手机迷”与性别有关.
解答 解:(1)由频率分布直方图可知,高一学生是“手机迷”的概率为P1=(0.0025+0.010)×20=0.25
由频数分布表可知,高二学生是“手机迷”的概率为${P_2}=\frac{14+4}{100}=0.18$
因为P1>P2,所以高一年级的学生是“手机迷”的概率大.…(5分)
(2)由频率分布直方图可知,在抽取的100人中,
“手机迷”有(0.010+0.0025)×20×100=25(人),非手机迷有100-25=75(人).
从而2×2列联表如下:
| 非手机迷 | 手机迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
点评 本题考查独立性检验以及概率的计算,考查基本知识的应用,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
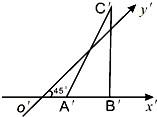 如图所示,△A′B′C′表示水平放置的△ABC在斜二测画法下的直观图,A′B′在x′轴上,B′C′与x′轴垂直,且B′C′=3,则△ABC的边AB上的高为6$\sqrt{2}$.
如图所示,△A′B′C′表示水平放置的△ABC在斜二测画法下的直观图,A′B′在x′轴上,B′C′与x′轴垂直,且B′C′=3,则△ABC的边AB上的高为6$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4} | B. | {2,4,8} | C. | {3,8} | D. | {1,3,5,7} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com