
分析 根据所给的等式,给变量赋值,求出a0+a2,a1+a3,即可得到所求的值.
解答 解:∵($\sqrt{5}$x-1)3=a0+a1x+a2x2+a3x3,
令x=-1,则(-$\sqrt{5}$-1)3=a0-a1+a2-a3=(a0+a2)-(a1+a3),…①
令x=1,($\sqrt{5}$x-1)3=a0+a1+a2+a3,…②,
解得a0+a2=$\frac{(\sqrt{5}-1)^{3}-(\sqrt{5}+1)^{3}}{2}$=-16,
a1+a3=$\frac{(\sqrt{5}-1)^{3}+(\sqrt{5}+1)^{3}}{2}$=8$\sqrt{5}$,
(a0+a2)2-(a1+a3)2=162-(8$\sqrt{5}$)2=-64.
故答案为:-64.
点评 本题考查二项式定理的性质,考查的是给变量赋值的问题,结合要求的结果,观察所赋得值,属于基础题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{7π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.如图表是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.
某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.如图表是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.| 时间分组 | 频数 |
| [0,20) | 12 |
| [20,40) | 20 |
| [40,60) | 24 |
| [60,80) | 26 |
| [80,100) | 14 |
| [100,120) | 4 |
| 非手机迷 | 手机迷 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:解答题
设等差数列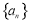 的前
的前 项和为
项和为 .且
.且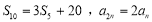 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令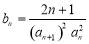 ,数列
,数列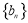 的前
的前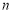 项和
项和 ,证明:对任意
,证明:对任意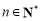 ,都有
,都有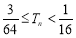 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com