
分析 (1)利用a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N*).分别取n=1,2,3,即可得出.
(2)利用递推关系可得:-Sn+2Sn-1+2=0,即Sn+2=2(Sn-1+2),利用等比数列的通项公式可得Sn,再利用递推关系可得an.
解答 (1)解:∵a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N*).
∴n=1时,a1=2;n=2时,2+2a2=1×(2+a2)+4,解得a2=4.
n=3时,2+2×4+3a3=2×(2+4+a3)+6,解得a3=8.
(2)证明:∵a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N*). ①
∴当n≥2时,a1+2a2+3a3+…+(n-1)an-1=(n-2)Sn-1+2(n-1).②
由①-②得nan=nan-Sn+2Sn-1+2,
∴-Sn+2Sn-1+2=0,即Sn+2=2(Sn-1+2),S1+2=4,
∴数列{Sn+2}是等比数列,以4为首项,2为公比.
∴Sn+2=2n+1.
∴n≥2时,an=Sn-Sn-1=2n+1-2-(2n-2)=2n.n=1时也成立.
∴an=2n.
点评 本题考查了数列递推关系、等比数列的通项公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源:2017届湖北省百所重点校高三联合考试数学(理)试卷(解析版) 题型:解答题
已知函数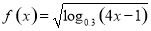 的定义域为
的定义域为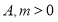 ,函数
,函数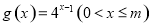 的值域为
的值域为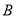 .
.
(1)当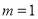 时,求
时,求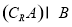 ;
;
(2)是否存在实数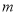 ,使得
,使得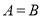 ?若存在,求出
?若存在,求出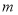 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知函数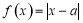 ,
,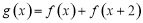 .
.
(Ⅰ)当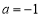 时,解不等式:
时,解不等式: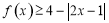 ;
;
(Ⅱ)若关于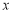 的不等式
的不等式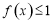 的解集为
的解集为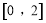 ,求证:
,求证: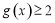 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
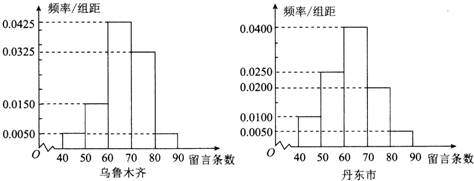
| 强烈关注 | 非常强烈关注 | 合计 | |
| 丹东市 | |||
| 乌鲁木齐市 | |||
| 合计 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com