练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．已知圆O的方程为x2+y2=4，过圆外一点P（3，$\sqrt{7}$）作圆O的两条切线，切点分别为T1和T2，则$\overrightarrow{P{T}_{1}}$•$\overrightarrow{P{T}_{2}}$=6．

    分析 根据直线与圆相切的性质可求PT1=PT2，及∠T1PT2，然后代入向量数量积的定义可求$\overrightarrow{P{T}_{1}}$•$\overrightarrow{P{T}_{2}}$．

    解答 解：由题意，OT1=OT2=2，PO=4，
    Rt△PT1O中，OT1=2，PO=4，PT1=2$\sqrt{3}$
    ∴∠OPT1=30°，∠T1PT2=2∠OPT1=60°
    ∴$\overrightarrow{P{T}_{1}}$•$\overrightarrow{P{T}_{2}}$=2$\sqrt{3}$$•2\sqrt{3}•\frac{1}{2}$=6
    故答案为：6

    点评 本题主要考查了圆的切线性质的应用及平面向量的数量积的定义的应用，属于基础试题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

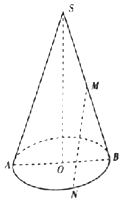    7．如图，平面SAB为圆锥的轴截面，O为底面圆的圆心，M为母线SB的中点，N为底面圆周上的一点，AB=4，SO=6．
    （1）求该圆锥的侧面积；
    （2）若直线SO与MN所成的角为30°，求MN的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．要得到函数 y=2cos x 的图象，只需将 y=2sin（ x-$\frac{π}{3}$） 的图象（　　）
    A．向右平移$\frac{5π}{6}$个单位B．向右平移$\frac{π}{3}$个单位
    C．向左平移$\frac{5π}{6}$个单位D．向左平移$\frac{π}{3}$个单位

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．如果函数y=logax（a＞0且a≠1）在[1，3]上的最大值与最小值的差为2，则满足条件的a值的集合是（　　）
    A．$\{\sqrt{3}\}$B．$\{\frac{{\sqrt{3}}}{3}\}$C．$\{\frac{{\sqrt{3}}}{3}，\sqrt{3}\}$D．$\{\sqrt{3}，3\}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知直线m：x=-4，圆M：x2+y2+2x-8=0，P为平面内一动点，若点P到圆心M的距离是到直线m距离的一半．
    （1）动点P的轨迹是什么曲线？写出该曲线的标准方程；
    （2）设动点P的轨迹为曲线F，过点E（4，-3）作直线l与曲线F交于C、D两点，并与直线x-y-1=0相交于点Q，问：$\frac{1}{|EC|}$、$\frac{1}{|EQ|}$、$\frac{1}{|ED|}$是否成等差数列？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．如图古铜钱外圆内方，外圆直径为4cm，中间是边长为1cm的正方形孔，随机地在古铜钱所在圆内任取一点，则该点刚好位于孔中的概率是$\frac{1}{4π}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．极坐标系的极点在平面直角坐标系的原点O处，极轴与x轴的正半轴重合，两坐标系单位长度相同．已知曲线的极坐标方程为ρ=2cosθ+2sinθ，直线l的参数方程为$\left\{\begin{array}{l}{x=2-t}\\{y=-1+t}\end{array}\right.$（t为参数）．
    （Ⅰ）将直线l的参数方程化为普通方程，将曲线C的极坐标方程化为直角坐标方程；
    （Ⅱ）设曲线C上到直线l的距离为d的点的个数为f（d），求f（d）的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$（a＞0，b＞0）的右焦点为F，过点F作x轴的垂线与双曲线交于B，C两点（点B在x轴上方），过点B作斜率为负数的渐近线的垂线，过点C作斜率为正数的渐近线的垂线，两垂线交于点D，若D到直线BC的距离等于虚轴长，则双曲线的离心率e等于（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．2D．$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知角α终边上一点P（-3，4），则cos（-π-α）的值为（　　）
    A．-$\frac{4}{3}$B．$\frac{4}{5}$C．$\frac{3}{5}$D．-$\frac{3}{5}$

    查看答案和解析>>

    同步练习册答案