
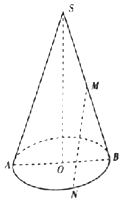
 如图,平面SAB为圆锥的轴截面,O为底面圆的圆心,M为母线SB的中点,N为底面圆周上的一点,AB=4,SO=6.
如图,平面SAB为圆锥的轴截面,O为底面圆的圆心,M为母线SB的中点,N为底面圆周上的一点,AB=4,SO=6.分析 (1)由题意知SO⊥平面ABN,在RT△SOB中,由条件和勾股定理求出母线BS,由圆锥的侧面积公式求出该圆锥的侧面积;
(2)取OB的中点C,连接MC、NC,由条件和中位线定理可得MC∥SO、MC的长,由条件和线面角的定理求出∠NMC,在RT△MCN中由余弦函数求出MN的长.
解答 解:(1)由题意知,SO⊥平面ABN,
在RT△SOB中,OB=$\frac{1}{2}$AB=2,SO=6,
∴BS=$\sqrt{{2}^{2}+{6}^{2}}$=$2\sqrt{10}$,
∴该圆锥的侧面积S=π•OB•BS=$4\sqrt{10}π$;
(2)取OB的中点C,连接MC、NC,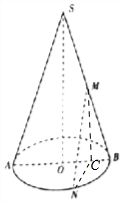
∵M为母线SB的中点,∴MC为△SOB的中位线,
∴MC∥SO,MC=$\frac{1}{2}$SO=3,
∵SO⊥平面ABN,∴MC⊥平面ABN,
∵NC?平面ABN,∴MC⊥NC,
∵直线SO与MN所成的角为30°,∴∠NMC=30°,
在RT△MCN中,$\frac{MC}{MN}=cos30°$,
∴MN=$\frac{MC}{cos30°}$=$\frac{3}{\frac{\sqrt{3}}{2}}$=$2\sqrt{3}$.
点评 本题考查圆锥的侧面积公式,线面角的定理,以及线面垂直的定义,属于中档题.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 5 | 7 | 13 | 19 |
| y | y1 | y2 | y3 | y4 | y5 |
| A. | 135 | B. | 90 | C. | 67 | D. | 63 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∵a∥α,b∥α,∴a∥b | B. | ∵a∥α,b?α,∴a∥b | C. | ∵α∥β,a∥β,∴a∥α | D. | ∵α∥β,a?β,∴a∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30°? | B. | 45°? | C. | 60°? | D. | 120°? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com