
 如图,矩形ACEF和等边三角形ABC中,AC=2,CE=1,平面ABC⊥平面ACEF.M是线段EF上的一个动点.
如图,矩形ACEF和等边三角形ABC中,AC=2,CE=1,平面ABC⊥平面ACEF.M是线段EF上的一个动点.分析 (1)M为线段EF的中点,证明:分别取AC、EF的中点O、M,连接OM,证明AC⊥BO,AC⊥OM,推出AC⊥面BOM,得到BM⊥AC;
(2)利用${V_{C-ABM}}={V_{B-ACM}}=\frac{1}{3}{S_{△ACM}}h$,转化求解即可.
解答  j解:(1)证明:M为线段EF的中点,理由如下:
j解:(1)证明:M为线段EF的中点,理由如下:
分别取AC、EF的中点O、M,连接OM,
在等边三角形ABC中,AC⊥BO,又OM为矩形ACEF的中位线,AC⊥OM,而OM∩OB=O,
所以AC⊥面BOM,所以BM⊥AC;
(2)由题${V_{C-ABM}}={V_{B-ACM}}=\frac{1}{3}{S_{△ACM}}h$,
由(1)和三角形ABC为等边三角形得O为AC的中点,
∴BO为三棱锥B-ACM的高h,
于是$h=\sqrt{3}$,
又∵无论M是EF上的何点,M到AC的距离不变,即为三角形ACM底边AC的高,
∴${S_{△ACM}}=\frac{1}{2}×2×1=1$,
∴${V_{C-ABM}}={V_{B-ACM}}=\frac{1}{3}×1×\sqrt{3}=\frac{{\sqrt{3}}}{3}$.
点评 本题考查集合体的体积的求法,直线与平面垂直的判定定理与性质的应用,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=4,BC=6,四边形AEFG为边长为2的正方形,现将矩形ABCD沿过点的动直线l翻折的点C在平面AEFG上的射影C1落在直线AB上,若点C在抓痕l上的射影为C2,则$\frac{{C}_{1}{C}_{2}}{C{C}_{2}}$的最小值为( )
如图,在矩形ABCD中,AB=4,BC=6,四边形AEFG为边长为2的正方形,现将矩形ABCD沿过点的动直线l翻折的点C在平面AEFG上的射影C1落在直线AB上,若点C在抓痕l上的射影为C2,则$\frac{{C}_{1}{C}_{2}}{C{C}_{2}}$的最小值为( )| A. | 6$\sqrt{5}$-13 | B. | $\sqrt{5}$-2 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 0 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30.4<40.2<log0.40.5 | B. | ${3^{0.4}}<{log_{0.4}}0.5<{4^{0.2}}$ | ||
| C. | ${log_{0.4}}0.5<{3^{0.4}}<{4^{0.2}}$ | D. | ${log_{0.4}}0.5<{4^{0.2}}<{3^{0.4}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AB⊥平面BCC1B1,$∠BC{C_1}=\frac{π}{3},AB=B{B_1}=2,BC=1,D$为CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AB⊥平面BCC1B1,$∠BC{C_1}=\frac{π}{3},AB=B{B_1}=2,BC=1,D$为CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
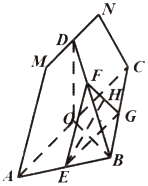 如图所示,四边形AMNC为等腰梯形,△ABC为直角三角形,平面AMNC与平面ABC垂直,AB=BC,AM=CN,点O、D、E分别是AC、MN、AB的中点.过点E作平行于平面AMNC的截面分别交BD、BC于点F、G,H是FG的中点.
如图所示,四边形AMNC为等腰梯形,△ABC为直角三角形,平面AMNC与平面ABC垂直,AB=BC,AM=CN,点O、D、E分别是AC、MN、AB的中点.过点E作平行于平面AMNC的截面分别交BD、BC于点F、G,H是FG的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com