
分析 先根据向量的数量积公式求出$\overrightarrow{a}$•$\overrightarrow{b}$=-4,再分别根据向量的数量积的运算和模计算即可.
解答 解:$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为120°,且|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=2,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos120°=4×2×(-$\frac{1}{2}$)=-4,
(1)($\overrightarrow{a}$-2$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=|$\overrightarrow{a}$|2-2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{a}$•$\overrightarrow{b}$-2|$\overrightarrow{b}$|2=16+4-2×4=12;
(2)|3$\overrightarrow{a}$-4$\overrightarrow{b}$|2=9|$\overrightarrow{a}$|2-24$\overrightarrow{a}$•$\overrightarrow{b}$+16|$\overrightarrow{b}$|2=9×42-24×(-4)+16×22=16×19,
∴|3$\overrightarrow{a}$-4$\overrightarrow{b}$|=4$\sqrt{19}$.
点评 本题考查了向量的数量积公式和向量的模,属于基础题.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(文)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知函数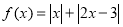 ,
,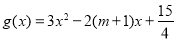 ;
;
(1)求不等式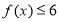 的解集;
的解集;
(2)若对任意的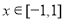 ,
,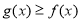 ,求
,求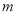 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{2}{5}+\frac{1}{5}i$ | B. | $\frac{2}{3}+\frac{1}{3}i$ | C. | $\frac{2}{3}-\frac{1}{3}i$ | D. | $-\frac{2}{5}-\frac{1}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{12}$或$\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<0} | B. | {x|x>1} | C. | {x|0<x≤1} | D. | {x|0≤x<1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com