
 如图,在三棱锥P-ABC中,PA⊥平面ABC,∠ACB=90°,F为线段PC上一点,E为线段PB上一点,PA=AB=2,AC=$\frac{{2\sqrt{3}}}{3}$,则当AF+FE取最小值时,AE与平面PBC所成角的正弦值为$\frac{3\sqrt{19}}{19}$.
如图,在三棱锥P-ABC中,PA⊥平面ABC,∠ACB=90°,F为线段PC上一点,E为线段PB上一点,PA=AB=2,AC=$\frac{{2\sqrt{3}}}{3}$,则当AF+FE取最小值时,AE与平面PBC所成角的正弦值为$\frac{3\sqrt{19}}{19}$. 分析 沿PB展开,使得A,F,E共面,则AE⊥PB时,AF+FE最小,求出AE,过P作AG⊥PC,则AG⊥平面PBC,∠AEG为AE与平面PBC所成角.
解答 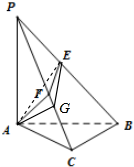 解:沿PB展开,使得A,F,E共面,则展开图中,AE⊥PB时,AF+FE最小,此时
解:沿PB展开,使得A,F,E共面,则展开图中,AE⊥PB时,AF+FE最小,此时
cos∠CPD=$\frac{\sqrt{6}}{3}$,sin∠CPD=$\frac{1}{3}$,∠CPA=30°,
∴cos∠APE=cos(∠CPD+30°)=$\frac{3\sqrt{2}-1}{6}$,
∴PE=$\frac{3\sqrt{2}-1}{3}$
由余弦定理可得AE=$\frac{\sqrt{19}}{3}$
∵PA⊥平面ABC,∠ACB=90°,
∴PC⊥BC,AC⊥BC,
∴BC⊥平面PAC,
过P作AG⊥PC,则AG⊥平面PBC,∠AEG为AE与平面PBC所成角,
∵PA=2,AC=$\frac{{2\sqrt{3}}}{3}$,∴PC=$\frac{4}{3}\sqrt{3}$,
由等面积可得2×$\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$AG,∴AG=1,
∴AE与平面PBC所成角的正弦值=$\frac{AG}{AE}$=$\frac{3\sqrt{19}}{19}$.
故答案为:$\frac{3\sqrt{19}}{19}$.
点评 本题考查线面角,考查学生的计算能力,正确作出线面角是关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | y=±$\frac{{2\sqrt{2}}}{3}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{{3\sqrt{2}}}{4}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,矩形ABCD所在平面与平面PAD垂直,PA⊥AD,且AD=2AB,E为BC上的动点.
如图,矩形ABCD所在平面与平面PAD垂直,PA⊥AD,且AD=2AB,E为BC上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com