
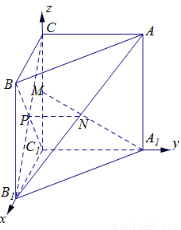
如图,已知三棱柱 的侧棱与底面垂直,且
的侧棱与底面垂直,且 ,
, ,
, ,点
,点 分别为
分别为 、
、 、
、 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)求二面角 的余弦值.
的余弦值.



(1)详见解析;(2)详见解析;(3)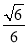 .
.
【解析】
试题分析:(1)线面平行的证明主要是走线面平行的判定定理这条路,因此必须在平面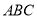 内寻找到一条与
内寻找到一条与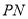 平行的直线,借助平几知识,这条直线不难找到;(2)在证明垂直关系时,如果几何证明有困难,也可从向量考虑;(3)求二面角的大小,主要是走向量这条路,它有固定步骤:首先求两个面的法向量,其次求法向量的余弦值进而得法向量的夹角,然后根据二面角是锐角还是钝角,决定其大小.
平行的直线,借助平几知识,这条直线不难找到;(2)在证明垂直关系时,如果几何证明有困难,也可从向量考虑;(3)求二面角的大小,主要是走向量这条路,它有固定步骤:首先求两个面的法向量,其次求法向量的余弦值进而得法向量的夹角,然后根据二面角是锐角还是钝角,决定其大小.
试题解析:(1)证明:连接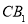 ,
,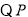 是
是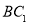 的中点 ,
的中点 ,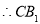 过点
过点 ,
,
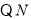 为
为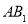 的中点,
的中点,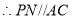 ,
,
又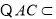 面
面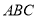 ,
,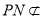 面
面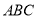 ,
,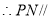 平面
平面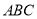 ;
;
(2)在直角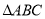 中,
中,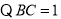 ,
,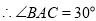 ,
,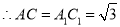 ,
,
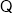 棱柱
棱柱 的侧棱与底面垂直,且
的侧棱与底面垂直,且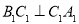 ,以点
,以点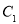 为原点,以
为原点,以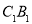 所在的直线为
所在的直线为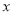 轴建立如图所示空间直角坐标系如图示,则
轴建立如图所示空间直角坐标系如图示,则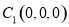 ,
,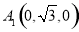 ,
,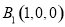 ,
,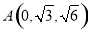 ,
,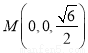 ,
,
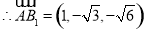 ,
,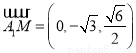 ,
,
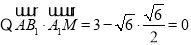 ,
,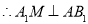 ;
;
(3)依题意得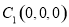 ,
,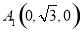 ,
,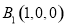 ,
,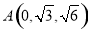 ,
,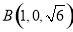 ,
,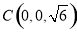 ,
,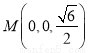 ,
, ,
,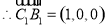
设面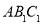 的一个法向量为
的一个法向量为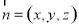 ,
,
由 ,得
,得 ,令
,令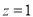 ,得
,得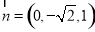 ,
,
同理可得面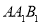 的一个法向量为
的一个法向量为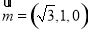 ,
,
故二面角的平面角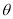 的余弦值为
的余弦值为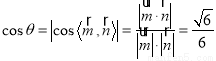 .
.
考点:空间向量与立体几何.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源:2015届四川成都树德中学高二3月月考文科数学试卷(解析版) 题型:解答题
如图,椭圆 经过点
经过点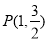 ,离心率
,离心率 ,直线
,直线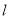 的方程为
的方程为 .
.

(1)求椭圆 的方程;
的方程;
(2) 是经过右焦点
是经过右焦点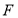 的任一弦(不经过点
的任一弦(不经过点 ),设直线
),设直线 与直线
与直线 相交于点
相交于点 ,记
,记 的斜率分别为
的斜率分别为 .问:是否存在常数
.问:是否存在常数 ,使得
,使得 ?若存在,求
?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市新高三起点调研考试文科数学试卷(解析版) 题型:选择题
如图为一个半球挖去一个圆锥的几何体的三视图,则该几何体的体积为( )
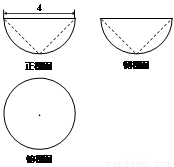
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知极坐标系的原点在直角坐标系的原点处,极轴为 轴正半轴,直线
轴正半轴,直线 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 .
.
(1)写出 的直角坐标方程,并说明
的直角坐标方程,并说明 是什么曲线?
是什么曲线?
(2)设直线 与曲线
与曲线 相交于
相交于 、
、 两点,求
两点,求 .
.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期中考试文科数学试卷(解析版) 题型:填空题
若函数 是定义在
是定义在 上的偶函数,且在区间
上的偶函数,且在区间 上是单调增函数.如果实数
上是单调增函数.如果实数 满足
满足 ,则
,则 的取值范围是 .
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com