解:(Ⅰ)由h(x)=

知,x∈[0,+∞),而h(0)=0,且h(1)=-1<0,h(2)=6-
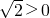
,则x=0为h(x)的一个零点,且h(x)在(1,2)内有零点,
∴h(x)至少有两个零点.
由h(x)=
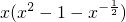
,记
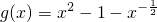
,则

,
当x∈(0,+∞)时,g(x)单调递增,故可判断出h(x)在(0,+∞)仅有一个零点,
综上所述,h(x)有且只有两个零点.
(Ⅱ)记h(x)的正零点为x
0,即
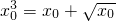
,
(1)当a<x
0时,由a
1=a,即a
1<x
0,而

,∴a
2<x
0.
由此猜测a
n<x
0.下面用数学归纳法证明:
①当n=1时,a
1<x
0,成立.
②假设当n=k时a
k<x
0成立,则当n=k+1时,由
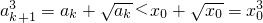
,知a
k+1<x
0.
因此当n=k+1时,a
k+1<x
0成立.
故对任意的n∈N
*,a
n≤x
0成立.
(2)当a≥x
0时,由(Ⅰ)知,当x∈(x
0,+∞)时,h(x)单调递增,∴h(a)h(x
0)=0,从而a
2≤a,由此猜测a
n≤a.下面用数学归纳法证明:
①当n=1时,a
1≤a,成立.
②假设当n=k时a
k<a成立,则当n=k+1时,由
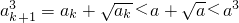
,知a
k+1<a.
因此当n=k+1时,a
k+1<a成立.故对任意的n∈N
*,a
n≤a成立.
综上所述,存在常数M,使得对于任意的n∈N
*,都有a
n≤M.
分析:(Ⅰ)由h(x)=

知,x∈[0,+∞),而h(0)=0,且h(1)=-1<0,h(2)=6-
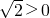
,再研究函数在(0,+∞)上的单调性,以确定零点个数即可
(Ⅱ)记h(x)的正零点为x
0,即
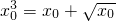
,当a<x
0时,由a
1=a,即a
1<x
0,而,a
2<x
0.由此猜测a
n<x
0.当a≥x
0时,由(Ⅰ)知,当x∈(x
1,+∞)时,h(x)单调递增,h(a)>h(x
0)=0,从而a
2<a,由此猜测a
n<a.然后用数学归纳法证明.
点评:本题考查数列的性质和运用,解题时要注意不等式性质的合理运用和数不归纳法的证明过程.

 .
. 知,x∈[0,+∞),而h(0)=0,且h(1)=-1<0,h(2)=6-
知,x∈[0,+∞),而h(0)=0,且h(1)=-1<0,h(2)=6-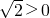 ,则x=0为h(x)的一个零点,且h(x)在(1,2)内有零点,
,则x=0为h(x)的一个零点,且h(x)在(1,2)内有零点,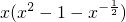 ,记
,记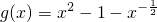 ,则
,则 ,
,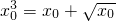 ,
, ,∴a2<x0.
,∴a2<x0.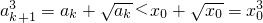 ,知ak+1<x0.
,知ak+1<x0.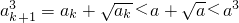 ,知ak+1<a.
,知ak+1<a. 知,x∈[0,+∞),而h(0)=0,且h(1)=-1<0,h(2)=6-
知,x∈[0,+∞),而h(0)=0,且h(1)=-1<0,h(2)=6-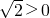 ,再研究函数在(0,+∞)上的单调性,以确定零点个数即可
,再研究函数在(0,+∞)上的单调性,以确定零点个数即可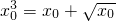 ,当a<x0时,由a1=a,即a1<x0,而,a2<x0.由此猜测an<x0.当a≥x0时,由(Ⅰ)知,当x∈(x1,+∞)时,h(x)单调递增,h(a)>h(x0)=0,从而a2<a,由此猜测an<a.然后用数学归纳法证明.
,当a<x0时,由a1=a,即a1<x0,而,a2<x0.由此猜测an<x0.当a≥x0时,由(Ⅰ)知,当x∈(x1,+∞)时,h(x)单调递增,h(a)>h(x0)=0,从而a2<a,由此猜测an<a.然后用数学归纳法证明.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<