解:①,根据题意,a=2,则f(x)=
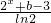
,
f′(x)=2
x>0,则f(x)在[0,+∞)为增函数,
故f(x)的最小值为f(0)=
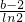
,其最大值不存在,则f(x)的值域为[
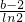
,+∞),
又由f(x)在[0,+∞)是“保值函数”,
则有
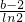
≥0,解可得b≥2;
故b的最小值为2.
②,根据题意,-1≤a≤1,且a≠0,-1≤b≤1,
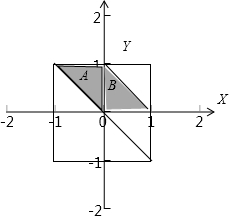
则a、b确定的区域为边长为2的正方形,其面积为4;
对于f(x),有f′(x)=2ax,x∈[0,1],
当-1≤a<0时,f′(x)<0,f(x)为减函数,
则f(x)的最大值为f(0)=b,最小值为f(1)=a+b,则f(x)的值域为[a+b,a],
若f(x)为保值函数,则有
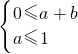
,
其表示的区域为阴影三角形A,面积为
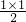
=

,
当0<a≤1时,f′(x)>0,f(x)为增函数,
则f(x)的最小值为f(0)=b,最大值为f(1)=a+b,则f(x)的值域为[a,a+b],
若f(x)为保值函数,则有
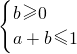
,
其表示的区域为阴影三角形B,面积为
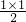
=

;
f(x)为保值函数对应区域的面积为1;
则f(x)为保值函数的概率为

;
故答案为①2,②

.
分析:①,由题意可得f(x)的解析式,对其求导判断可得f(x)为增函数,进而可得f(x)的值域,根据题意中保值函数的定义,可得
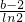
≥0,解可得b的范围,即可得答案.
②,根据题意,由a、b的范围分析可得其表示的平面区域,计算可得其面积,对于函数f(x),分-1≤a<0与0<a≤1两种情况,先分析出f(x)的单调性,由此得到f(x)的值域,进而由保值函数的定义,可得关于a、b的不等式组,分析可得其对应的平面区域,易得其面积,综合两种情况可得f(x)为保值函数对应的平面区域即面积,由几何概型公式计算可得答案.
点评:本题考查几何概型的计算以及函数单调性的应用,关键是理解保值函数的定义.

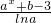 ,g(x)=ax2+b.
,g(x)=ax2+b.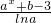 是[0,+∞)内的“保值函数”,则b的最小值为________;
是[0,+∞)内的“保值函数”,则b的最小值为________;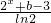 ,
,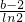 ,其最大值不存在,则f(x)的值域为[
,其最大值不存在,则f(x)的值域为[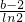 ,+∞),
,+∞),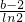 ≥0,解可得b≥2;
≥0,解可得b≥2;
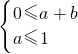 ,
,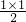 =
= ,
,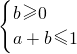 ,
,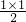 =
= ;
; ;
; .
.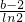 ≥0,解可得b的范围,即可得答案.
≥0,解可得b的范围,即可得答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案