
【题目】已知![]() ,
,![]() .
.
(1)求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若![]() ,证明
,证明![]() 在
在![]() 上单调递增;
上单调递增;
(3)设![]() 对任意
对任意![]() ,
,![]() 成立求实数k的取值范围.
成立求实数k的取值范围.
科目:高中数学 来源: 题型:
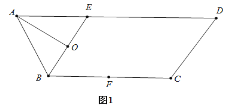
【题目】如图1,等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,O为BE中点,F为BC中点.将
,O为BE中点,F为BC中点.将![]() 沿BE折起到
沿BE折起到![]() 的位置,如图2.
的位置,如图2.
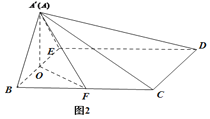
(1)证明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面BCDE,求点F到平面
平面BCDE,求点F到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,过右焦点作平行于一条渐近线的直线交双曲线于点
,过右焦点作平行于一条渐近线的直线交双曲线于点![]() ,若
,若![]() 的内切圆半径为
的内切圆半径为![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体有8个不同顶点,现任意选择其中4个不同顶点,然后将它们两两相连,可组成平面图形成空间几何体.在组成的空间几何体中,可以是下列空间几何体中的________.(写出所有正确结论的编号)
①每个面都是直角三角形的四面体;
②每个面都是等边三角形的四面体;
③每个面都是全等的直角三角形的四面体;
④有三个面为等腰直角三角形,有一个面为等边三角形的四面体.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=2AB=4,E为BC的中点,现将△BAE与△DCE折起,使得平面BAE及平面DEC都与平面ADE垂直.

(1)求证:BC∥平面ADE;
(2)求二面角A﹣BE﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com