
设f(x)和g(x)都是定义在同一区间上的两个函数,若对任意x∈[1,2],都有|f(x)+g(x)|≤8,则称f(x)和g(x)是“友好函数”,设f(x)=ax,g(x)=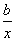 .
.
(1)若a∈{1,4},b∈{-1,1,4},求f(x)和g(x)是“友好函数”的概率;
(2)若a∈[1,4],b∈[1,4],求f(x)和g(x)是“友好函数”的概率.
解析: (1)设事件A表示f(x)和g(x)是“友好函数”,
则|f(x)+g(x)|(x∈[1,2])所有的情况有:
x-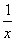 ,x+
,x+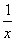 ,x+
,x+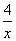 ,4x-
,4x-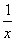 ,4x+
,4x+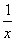 ,4x+
,4x+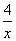 ,
,
共6种且每种情况被取到的可能性相同.
又当a>0,b>0时,ax+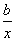 在
在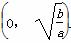 上递减,在
上递减,在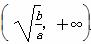 上递增;
上递增;
x-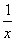 和4x-
和4x-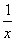 在(0,+∞)上递增,
在(0,+∞)上递增,
∴对x∈[1,2]可使|f(x)+g(x)|≤8恒成立的有x-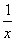 ,x+
,x+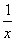 ,x+
,x+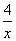 ,4x-
,4x-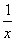 ,故事件A包含的基本事件有4种,
,故事件A包含的基本事件有4种,
∴P(A)= =
= ,故所求概率是
,故所求概率是 .
.
(2)设事件B表示f(x)和g(x)是“友好函数”,
∵a是从区间[1,4]中任取的数,b是从区间[1,4]中任取的数,
∴点(a,b)所在区域是长为3,宽为3的矩形区域.
要使x∈[1,2]时,|f(x)+g(x)|≤8恒成立,
需f(1)+g(1)=a+b≤8且f(2)+g(2)=2a+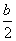 ≤8,
≤8,
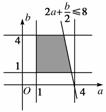
∴事件B表示的点的区域是如图所示的阴影部分.
∴P(B)=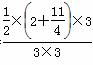 =
=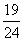 ,
,
故所求概率是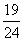 .
.


科目:高中数学 来源: 题型:
已知向量a=(cosλθ,cos(10-λ)θ),b=(sin(10-λ)θ,sinλθ),λ、θ∈R.
(1) 求|a|2+|b|2的值;
(2) 若a⊥b,求θ;
(3) 若θ=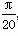 ,求证:a∥b.
,求证:a∥b.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知平面α、β和直线m,给出条件:
①m∥α;②m⊥α;③m⊂α;④α⊥β;⑤α∥β.
(1)当满足条件________时,有m∥β;
(2)当满足条件________时,有m⊥β.(填所选条件的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则( )
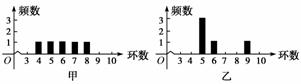
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的方差小于乙的成绩的方差
D.甲的成绩的极差小于乙的成绩的极差
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A、B、C三个箱子中各装有两个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出一个球.
(1)若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(2)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l过抛物线y2=4x的焦点F,交抛物线于A、B两点,且点A、B到y轴的距离分别为m,n,则m+n+2的最小值为( )
A.4 B.6
B.6
C.4 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com