
已知向量a、b的夹角为45°,且|a|=1,|2a-b|=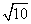 ,则|b|=( )
,则|b|=( )
A.3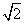 B.2
B.2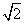 C.
C.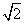 D.1
D.1
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
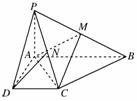
如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=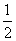 AB=1,M是PB的中点.
AB=1,M是PB的中点.
(1)求证:AM=CM;
(2)若N是PC的中点,求证:DN∥平面AMC.
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)和g(x)都是定义在同一区间上的两个函数,若对任意x∈[1,2],都有|f(x)+g(x)|≤8,则称f(x)和g(x)是“友好函数”,设f(x)=ax,g(x)=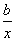 .
.
(1)若a∈{1,4},b∈{-1,1,4},求f(x)和g(x)是“友好函数”的概率;
(2)若a∈[1,4],b∈[1,4],求f(x)和g(x)是“友好函数”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知△ABC的内角为A、B、C,其对边分别为a、b、c,B为锐角,向量m=(2sin B,-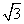 ),n=
),n=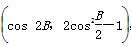 ,且m∥n.
,且m∥n.
(1)求角B的大小;
(2)如果b=2,求S△ABC的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为 .过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为________.
.过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(1)当a=-2时,求不等式f(x)<g(x)的解集;
(2)设a>-1时,且当x∈ 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com