练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知向量a=(1,3),b=(-2,-6),|c|=,若(a+b)·c=5,则a与c的夹角为__________.

     

    θ=120°

    【解析】设c=(x,y),因为a+b=(-1,-3),

    所以(a+b)·c=-x-3y=5,|c|==,即

    解得或

    不妨取即c=,

    设a与c的夹角为θ,

    则cosθ==

    =-.

    因为0°≤θ≤180°,所以θ=120°.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学考前复习冲刺穿插滚动练习（二）（解析版） 题型：解答题

    已知△ABC的内角A、B、C的对边分别为a、b、c，sin Ccos C－cos2C＝，且c＝3.

    (1)求角C；

    (2)若向量m＝(1，sin A)与n＝(2，sin B)共线，求a、b的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学考前复习冲刺穿插滚动练习（一）（解析版） 题型：解答题

    某造纸厂拟建一座底面图形为矩形且面积为162平方米的三级污水处理池，池的深度一定(平面图如图所示)，如果池四周围墙建造单价为400元/米，中间两道隔墙建造单价为248元/米，池底建造单价为80元/平方米，水池所有墙的厚度忽略不计．

    (1)试设计污水处理池的长和宽，使总造价最低，并求出最低总造价；

    (2)若由于地形限制，该池的长和宽都不能超过16米，试设计污水处理池的长和宽，使总造价最低，并求出最低总造价．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学考前复习冲刺穿插滚动练习（一）（解析版） 题型：选择题

    设a＝log54，b＝(log53)2，c＝log45，则 (　　)

    A．a<c<b B．b<c<a

    C．a<b<c D．b<a<c

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第四章平面向量、数系扩充与复数引入（解析版） 题型：解答题

    已知复平面内平行四边形ABCD(A,B,C,D按逆时针排列),A点对应的复数为2+i,向量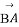对应的复数为1+2i,向量对应的复数为3-i.

    (1)求点C,D对应的复数.

    (2)求平行四边形ABCD的面积.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第四章平面向量、数系扩充与复数引入（解析版） 题型：选择题

    (2014·宁波模拟)在平面直角坐标系中,A(,1),B点是以原点O为圆心的单位圆上的动点,则|+|的最大值是(　　)

    A.4 B.3 C.2 D.1

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第四章平面向量、数系扩充与复数引入（解析版） 题型：选择题

    (2014·孝感模拟)已知下列结论：

    ①若a=b,b=c,则a=c;

    ②若a∥b,b∥c,则a∥c;

    ③|a·b|=|a|·|b|;

    ④若a·b=a·c,则b=c的逆命题.

    其中正确的是(　　)

    A.①② B.①④ C.①②③ D.①②④

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第十章 算法初步、统计、统计案例（解析版） 题型：选择题

    (2014·营口模拟)一个路口的信号灯,绿灯亮40秒后,黄灯亮若干秒,然后红灯亮30秒,如果一辆车到达路口时,遇到红灯的概率为,那么黄灯亮的时间为

    (　　)

    A.3秒 B.4秒 C.5秒 D.6秒

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第八章 平面解析几何（解析版） 题型：选择题

    设双曲线-=1(a>0,b>0)的右焦点为F,过点F作与x轴垂直的直线l交两渐近线于A,B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若=λ+μ(λ,μ∈R),λμ=,则该双曲线的离心率为(　　)

    A. B. C. D.

     

    查看答案和解析>>

    同步练习册答案