练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (2014·孝感模拟)已知下列结论：

    ①若a=b,b=c,则a=c;

    ②若a∥b,b∥c,则a∥c;

    ③|a·b|=|a|·|b|;

    ④若a·b=a·c,则b=c的逆命题.

    其中正确的是(　　)

    A.①② B.①④ C.①②③ D.①②④

     

    B

    【解析】由向量相等的概念知①正确;

    因为零向量和任何向量共线,

    所以当b=0时,结论②不成立,故②不正确;

    因为|a·b|=|a||b||cosθ|(θ是a与b的夹角),

    所以当|cosθ|≠1时,③不正确;④的逆命题是“若b=c,则a·b=a·c”,显然该结论是正确的.故选B.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学考前复习冲刺穿插滚动练习（二）（解析版） 题型：选择题

    某车间分批生产某种产品，每批的生产准备费用为800元．若每批生产x件，则平均仓储时间为天，且每件产品每天的仓储费用为1元．为使平均到每件产品的生产准备费用与仓储费用之和最小，每批应生产产品(　　)

    A．60件 B．80件 C．100件 D．120件

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学考前复习冲刺穿插滚动练习（一）（解析版） 题型：选择题

    设f(x)是定义在实数集R上的函数，满足条件y＝f(x＋1)是偶函数，且当x≥1时，f(x)＝()x－1，则f()，f()，f()的大小关系是 (　　)

    A．f()>f()>f()

    B．f()>f()>f()

    C．f()>f()>f()

    D．f()>f()>f()

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第四章平面向量、数系扩充与复数引入（解析版） 题型：填空题

    已知向量a=(1,3),b=(-2,-6),|c|=,若(a+b)·c=5,则a与c的夹角为__________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第四章平面向量、数系扩充与复数引入（解析版） 题型：选择题

    下面是关于复数z=+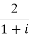的四个命题：

    p1：|z|=2;p2：z2=4i;p3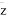：=2i;p4：z的虚部是0,其中的真命题为(　　)

    A.p1,p2 B.p1,p3 C.p2,p3 D.p3,p4

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第十章 算法初步、统计、统计案例（解析版） 题型：解答题

    (2014·泰安模拟)某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示：

    锻炼时间

    (分钟)

    [0,20)

    [20,40)

    [40,60)

    [60,80)

    [80,100)

    [100,120)

    人数

    40

    60

    80

    100

    80

    40

    现采用分层抽样的方法抽取容量为20的样本.

    (1)其中课外体育锻炼时间在分钟内的学生应抽取多少人?

    (2)若从(1)中被抽取的学生中随机抽取2名,求这2名学生课外体育锻炼时间均在分钟内的概率.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第十章 算法初步、统计、统计案例（解析版） 题型：填空题

    (2014·天门模拟)在区间[0,4]内随机取两个数a,b,则使得函数f(x)=x2+ax+b2有零点的概率为________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第六章 不等式、推理与证明（解析版） 题型：填空题

    对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义：f′′(x)是函数y=f(x)的导数f′(x)的导数,若方程f′′(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有′拐点′;任何一个三次函数都有对称中心,且‘拐点’就是对称中心”.请你将这一发现作为条件,则函数f(x)=x3-3x2+3x的对称中心为__________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第五章 数列（解析版） 题型：解答题

    已知数列{an}为等差数列,a3=5,a7=13,数列{bn}的前n项和为Sn,且有Sn=2bn-1,

    (1)求{an},{bn}的通项公式.

    (2)若cn=anbn,{cn}的前n项和为Tn,求Tn.

     

    查看答案和解析>>

    同步练习册答案