
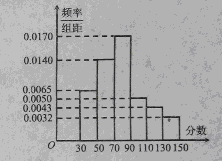
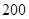 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于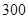 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.| 寿命(天) | 频数 | 频率 |
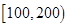 | 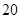 | 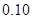 |
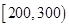 | 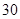 | 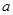 |
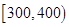 | 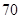 | 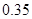 |
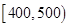 | 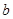 | 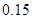 |
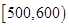 | 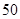 | 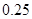 |
| 合计 | 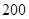 | 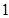 |
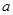 、
、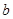 的值;
的值;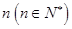 个,如果这
个,如果这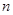 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求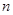 的最小值;
的最小值;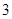 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用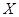 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求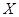 的分布列和数学期望.
的分布列和数学期望.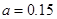 ,
,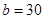 ;(2)
;(2)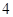 ;(3)详见解析.
;(3)详见解析.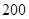 以及频率之和为
以及频率之和为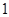 分别求出
分别求出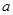 、
、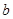 的值;(2)先确定灯泡中优等品、正品、次品的个数,计算三者之间的比例,从而确定灯泡数的表达式,进而确定
的值;(2)先确定灯泡中优等品、正品、次品的个数,计算三者之间的比例,从而确定灯泡数的表达式,进而确定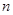 的最小值;(3)先确定随机变量
的最小值;(3)先确定随机变量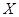 的可能取值,根据题中条件确定
的可能取值,根据题中条件确定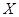 在不同取值下的概率,并列出相应的分布列,求出数学期望.
在不同取值下的概率,并列出相应的分布列,求出数学期望.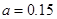 ,
,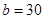 .
.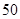 个,正品有
个,正品有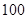 个,次品有
个,次品有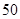 个,
个,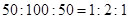 .
.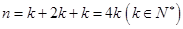 ,
,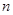 的最小值为
的最小值为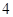 ;
;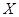 的所有取值为
的所有取值为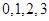 .
.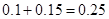 ,
,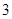 个,可看成
个,可看成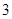 次独立重复试验,
次独立重复试验,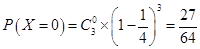 ,
,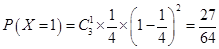 ,
,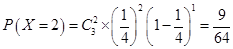 ,
,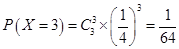 .
.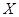 的分布列为:
的分布列为: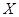 |  | 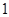 | 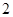 | 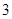 |
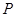 | 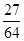 | 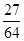 |  | 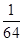 |
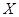 的数学期望
的数学期望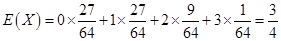 .
.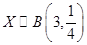 ,
,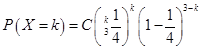 ,
,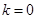 、
、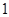 、
、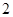 、
、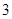 .请酌情给分)
.请酌情给分)

科目:高中数学 来源:不详 题型:解答题
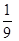 ,求甲在初赛中答题个数
,求甲在初赛中答题个数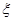 的分布列及数学期望
的分布列及数学期望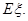 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 的把握认为对莫言作品的非常了解与性别有关?
的把握认为对莫言作品的非常了解与性别有关?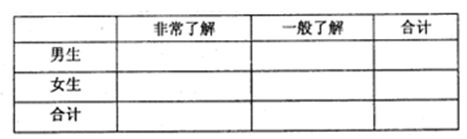

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题


 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 转速x/(rad/s) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y/件 | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| | 杂质高 | 杂质低 |
| 旧设备 | 37 | 121 |
| 新设备 | 22 | 202 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
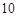 分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样; ;
; 与
与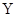 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“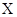 与
与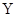 有关系”的把握越大.其中真命题的序号为( )
有关系”的把握越大.其中真命题的序号为( )| A.①④ | B.②④ | C.①③ | D.②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 ,求恰有一名同学获得该高校B类资格的概率.
,求恰有一名同学获得该高校B类资格的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com