
| | 杂质高 | 杂质低 |
| 旧设备 | 37 | 121 |
| 新设备 | 22 | 202 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
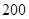 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于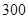 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.| 寿命(天) | 频数 | 频率 |
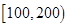 | 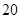 | 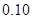 |
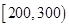 | 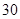 | 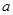 |
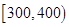 | 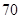 | 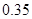 |
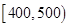 | 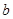 | 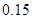 |
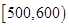 | 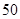 | 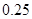 |
| 合计 | 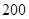 | 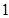 |
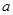 、
、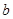 的值;
的值;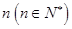 个,如果这
个,如果这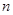 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求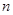 的最小值;
的最小值;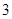 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用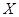 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求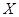 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
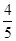 ,则每个学生补习的概率为( )
,则每个学生补习的概率为( )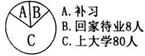
A.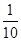 | B.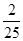 | C.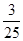 | D.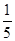 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 气温x(°C) | 18 | 13 | 10 | -1 |
| 山高y(km) | 24 | 34 | 38 | 64 |
 ,由此请估计出山高为72(km)处气温的度数为( )
,由此请估计出山高为72(km)处气温的度数为( )查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 年份 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 |
| x(kg) | 70 | 74 | 80 | 78 | 85 | 92 | 90 | 95 |
| y(t) | 5.1 | 6.0 | 6.8 | 7.8 | 9.0 | 10.2 | 10.0 | 12.0 |
| | ||||||||
| 年份 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | |
| x(kg) | 92 | 108 | 115 | 123 | 130 | 138 | 145 | |
| y(t) | 11.5 | 11.0 | 11.8 | 12.2 | 12.5 | 12.8 | 13.0 | |
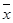 =101,
=101,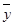 ≈10.113 3,
≈10.113 3,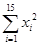 =161 125,
=161 125,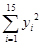 =1 628.55,
=1 628.55,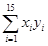 =16 076.8)
=16 076.8)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
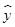 =0.50x-0.81,则x=25时,
=0.50x-0.81,则x=25时,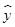 为11.69
为11.69查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 又发作过心脏病 | 未发作过心脏病 | 合计 |
| 心脏搭桥手术 | 39 | 157 | 196 |
| 血管清障手术 | 29 | 167 | 196 |
| 合计 | 68 | 324 | 392 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com