
| 气温x(°C) | 18 | 13 | 10 | -1 |
| 山高y(km) | 24 | 34 | 38 | 64 |
 ,由此请估计出山高为72(km)处气温的度数为( )
,由此请估计出山高为72(km)处气温的度数为( ) 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
| x | 35 | 40 | 45 | 50 |
| y | 56 | 41 | 28 | 11 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
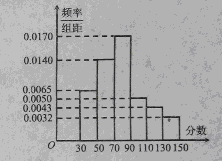
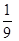 ,求甲在初赛中答题个数
,求甲在初赛中答题个数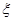 的分布列及数学期望
的分布列及数学期望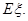 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190] |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高(cm) | [150,155) | [150,160) | [160,165) | [165,170) | [170,175) | [175,180] |
| 频数 | 2 | 12 | 16 | 6 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 转速x/(rad/s) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y/件 | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求甲在初赛中答题个数的分布列和数学期望.
,求甲在初赛中答题个数的分布列和数学期望.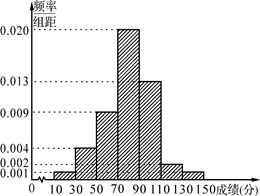
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
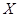 与
与 是否有关系时,通过查阅下表来确定“
是否有关系时,通过查阅下表来确定“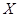 和
和 有关系”的可信度。如果
有关系”的可信度。如果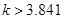 ,那么就有把握认为“
,那么就有把握认为“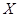 和
和 有关系”的百分比为( )
有关系”的百分比为( ) |  |  |  |  |  |  |  |  |  |  |
 |  |  | 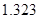 |  |  |  |  |  |  |  |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| | 杂质高 | 杂质低 |
| 旧设备 | 37 | 121 |
| 新设备 | 22 | 202 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 ,求恰有一名同学获得该高校B类资格的概率.
,求恰有一名同学获得该高校B类资格的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com