
(本题满分14分)已知两点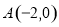 、
、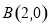 ,动点
,动点 与
与 、
、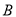 两点连线的斜率
两点连线的斜率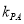 、
、 满足
满足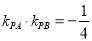 .
.
(Ⅰ)求动点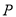 的轨迹
的轨迹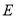 的方程;
的方程;
(Ⅱ)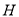 是曲线
是曲线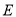 与
与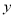 轴正半轴的交点,曲线
轴正半轴的交点,曲线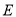 上是否存在两点
上是否存在两点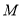 、
、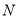 ,使得
,使得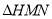 是以
是以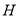 为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
(Ⅰ)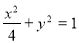 (
( );(Ⅱ)3个
);(Ⅱ)3个
【解析】
试题分析:(Ⅰ)求动点的轨迹方程的一般步骤:1.建系——建立适当的坐标系.2.设点——设轨迹上的任一点P(x,y).3.列式——列出动点P所满足的关系式.4.代换——依条件式的特点,选用距离公式、斜率公式等将其转化为x,y的方程式,并化简.5.证明——证明所求方程即为符合条件的动点的轨迹方程.
(Ⅱ)由题意可知设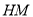 所在直线的方程为
所在直线的方程为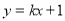 ,则
,则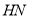 所在直线的方程为
所在直线的方程为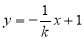 分别联立椭圆方程求得弦长
分别联立椭圆方程求得弦长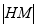 ,
,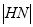 ,再由
,再由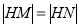 得
得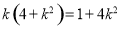 解方程即可
解方程即可
试题解析:(Ⅰ)设点 的坐标为
的坐标为 (
( ),则
),则 ,
, , 2分
, 2分
依题意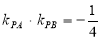 ,所以
,所以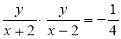 ,化简得
,化简得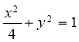 , 4分
, 4分
所以动点 的轨迹
的轨迹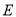 的方程为
的方程为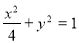 (
( ). 5分
). 5分
注:如果未说明 (或注
(或注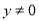 ),扣1分.
),扣1分.
(Ⅱ)设能构成等腰直角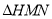 ,其中
,其中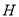 为
为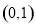 ,
,
由题意可知,直角边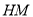 ,
,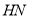 不可能垂直或平行于
不可能垂直或平行于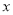 轴,故可设
轴,故可设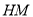 所在直线的方程为
所在直线的方程为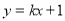 ,
,
(不妨设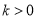 ),则
),则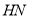 所在直线的方程为
所在直线的方程为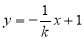 7分
7分
联立方程 ,消去
,消去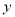 整理得
整理得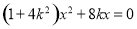 ,解得
,解得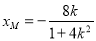 ,
,
将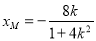 代入
代入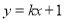 可得
可得 ,故点
,故点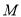 的坐标为
的坐标为 .
.
所以 , 9分
, 9分
同理可得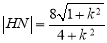 ,由
,由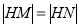 ,得
,得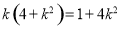 ,
,
所以 ,整理得
,整理得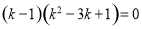 ,解得
,解得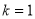 或
或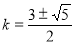 11分
11分
当 斜率
斜率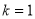 时,
时,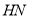 斜率
斜率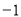 ;当
;当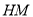 斜率
斜率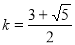 时,
时,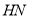 斜率
斜率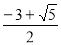 ;
;
当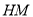 斜率
斜率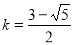 时,
时,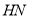 斜率
斜率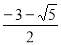 ,
,
综上所述,符合条件的三角形有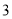 个. 14分
个. 14分
考点:圆锥曲线的综合应用


科目:高中数学 来源:2014-2015学年河北邢台一中高二上学期期中考试文科数学试卷(解析版) 题型:选择题
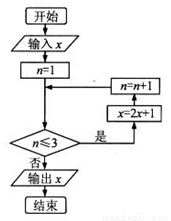
已知实数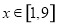 ,执行如图所示的程序框图,则输出的x不小于55的概率为( )
,执行如图所示的程序框图,则输出的x不小于55的概率为( )
A.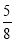 B.
B.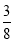 C.
C.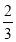 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省山一等七校高三12月联考文科数学试卷(解析版) 题型:填空题
函数 的图象中相邻两条对称轴的距离为____________________________.
的图象中相邻两条对称轴的距离为____________________________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省山一等七校高三12月联考文科数学试卷(解析版) 题型:选择题
已知实数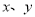 满足约束条件
满足约束条件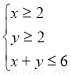 ,则
,则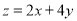 的最大值为( ).
的最大值为( ).
A.24 B.20 C.16 D.12
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省山一等七校高三12月联考理科数学试卷(解析版) 题型:选择题
由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集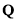 划分为两个非空的子集
划分为两个非空的子集 与
与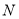 ,且满足
,且满足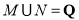 ,
,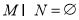 ,
, 中的每一个元素都小于
中的每一个元素都小于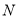 中的每一个元素,则称
中的每一个元素,则称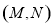 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割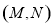 ,下列选项中,不可能成立的是( )
,下列选项中,不可能成立的是( )
A. 没有最大元素,
没有最大元素,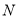 有一个最小元素
有一个最小元素
B. 没有最大元素,
没有最大元素,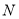 也没有最小元素
也没有最小元素
C. 有一个最大元素,
有一个最大元素,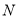 有一个最小元素
有一个最小元素
D. 有一个最大元素,
有一个最大元素,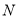 没有最小元素
没有最小元素
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省四地六校高三上学期第三次月考文科数学试卷(解析版) 题型:选择题
已知定义在R上的函数 的图象关于点
的图象关于点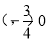 成中心对称图形,且满足
成中心对称图形,且满足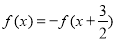 ,
,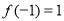 ,
,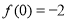 ,则
,则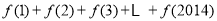 的值为( )
的值为( )
A.1 B.2 C. 0? D.-2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com