
由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集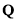 划分为两个非空的子集
划分为两个非空的子集 与
与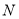 ,且满足
,且满足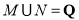 ,
,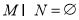 ,
, 中的每一个元素都小于
中的每一个元素都小于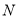 中的每一个元素,则称
中的每一个元素,则称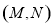 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割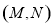 ,下列选项中,不可能成立的是( )
,下列选项中,不可能成立的是( )
A. 没有最大元素,
没有最大元素,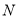 有一个最小元素
有一个最小元素
B. 没有最大元素,
没有最大元素,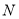 也没有最小元素
也没有最小元素
C. 有一个最大元素,
有一个最大元素,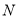 有一个最小元素
有一个最小元素
D. 有一个最大元素,
有一个最大元素,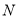 没有最小元素
没有最小元素
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年河南省高二上学期第一次月考试理科数学卷(解析版) 题型:填空题
在△ABC中,角A、B、C的对边分别为a、b、c,且a=8,B=60°,C=75°,则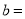 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省山一等七校高三12月联考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数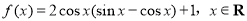 .
.
(1)求函数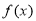 的最小正周期;
的最小正周期;
(2)求函数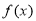 在区间
在区间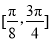 上的最小值和最大值.
上的最小值和最大值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省山一等七校高三12月联考理科数学试卷(解析版) 题型:解答题
(本题满分14分)已知两点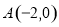 、
、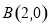 ,动点
,动点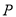 与
与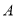 、
、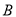 两点连线的斜率
两点连线的斜率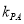 、
、 满足
满足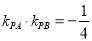 .
.
(Ⅰ)求动点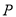 的轨迹
的轨迹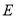 的方程;
的方程;
(Ⅱ)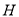 是曲线
是曲线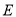 与
与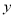 轴正半轴的交点,曲线
轴正半轴的交点,曲线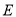 上是否存在两点
上是否存在两点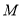 、
、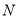 ,使得
,使得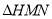 是以
是以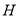 为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省山一等七校高三12月联考理科数学试卷(解析版) 题型:填空题
已知 为
为 平面内的一个区域.
平面内的一个区域.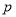 :点
:点 ;
;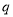 :点
:点 .如果
.如果 是
是 的充分条件,那么区域
的充分条件,那么区域 的面积的最小值是_________.
的面积的最小值是_________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测文科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,已知PA?⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC=PA,E是PC的中点,F是PB的中点.
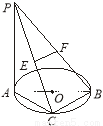
(1)求证:EF//平面ABC;
(2)求证:EF?平面PAC;
(3)求三棱锥B—PAC的体积.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测理科数学试卷(解析版) 题型:解答题
(本小题满分14分)如图,四棱柱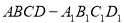 中,
中,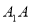 ?底面ABCD,且
?底面ABCD,且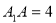 . 梯形ABCD的面积为6,且AD//BC,AD=2BC,
. 梯形ABCD的面积为6,且AD//BC,AD=2BC,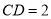 . 平面
. 平面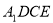 与
与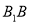 交于点E.
交于点E.

(1)证明:EC//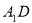 ;
;
(2)求三棱锥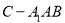 的体积;
的体积;
(3)求二面角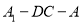 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省四地六校高三上学期第三次月考理科数学试卷(解析版) 题型:解答题
将12cm长的细铁线截成三条长度分别为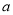 、
、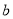 、
、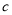 的线段,
的线段,
(1)求以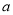 、
、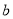 、
、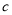 为长、宽、高的长方体的体积的最大值;
为长、宽、高的长方体的体积的最大值;
(2)若这三条线段分别围成三个正三角形,求这三个正三角形面积和的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com