练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知角α终边逆时针旋转 与单位圆交于点 ，且 ．
    （1）求 的值，
    （2）求 的值．

    【答案】
    （1）解：角α终边逆时针旋转 与单位圆交于点 ，

    可得sin（ ）= ，

    cos（ ）= ，

    sin（2 ）=2sin（ ）cos（ ）= = ，

    cos（2 ）=2× = ．

    =sin（2 ﹣ ）=sin（2 ）cos ﹣sin cos（2 ）= = ．


    （2）解：∵ ，∴tan（2α+2β）= = = ．

    sin（2 ）= ，

    cos（2 ）= ．

    tan（2 ）= ．

    tan（2α+2β）=tan[（ ）+（2 ）]= = ，

    解得 =


    【解析】（1）利用已知条件求出sin（ ）与cos（ ），然后利用二倍角公式以及两角和的正弦函数化简求解即可．（2）求出正切函数的二倍角的值，利用两角和的正切函数化简求解即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】解答
    （1）在公比为2的等比数列{an}中，a2与a5的等差中项是9 ．求a1的值；
    （2）若函数y=a1sin（ φ），0＜φ＜π的一部分图象如图所示，M（﹣1，a1），N（3，﹣a1）为图象上的两点，设∠MON=θ，其中O为坐标原点，0＜θ＜π，求cos（θ﹣φ）的值．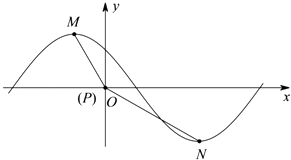

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在斜三棱柱ABC﹣A1B1C1中，侧面ACC1A1与侧面CBB1C1都是菱形，∠ACC1=∠CC1B1=60°，AC=2．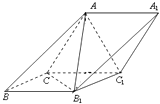

    （1）求证：AB1⊥CC1；
    （2）若 ，求二面角C﹣AB1﹣A1的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D．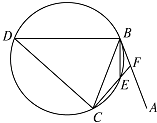

    （1）证明：DB=DC；
    （2）设圆的半径为1，BC=3，延长CE交AB于点F，求△BCF外接圆的半径．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，AB=3，AC=4，N是AB的中点，边AC（含端点）上存在点M，使得BM⊥CN，则cosA的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某房地产开发公司计划在一楼区内建造一个长方形公园ABCD，公园由形状为长方形A1B1C1D1的休闲区和环公园人行道(阴影部分)组成．已知休闲区A1B1C1D1的面积为4000平方米，人行道的宽分别为4米和10米(如图所示)．

    (1)若设休闲区的长和宽的比＝x(x>1)，求公园ABCD所占面积S关于x的函数S(x)的解析式；

    (2)要使公园所占面积最小，则休闲区A1B1C1D1的长和宽该如何设计？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】解答
    （1）若ax＞lnx恒成立，求实数a的取值范围；
    （2）证明：a＞0，x0∈R，使得当x＞x0时，ax＞lnx恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

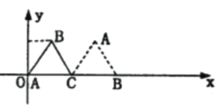
    【题目】如图放置的边长为2的正三角形沿轴滚动, 设顶点的纵坐标与横坐标的函数关系式是， 有下列结论:

    ①函数的值域是；②对任意的，都有；

    ③函数是偶函数；④函数单调递增区间为.

    其中正确结论的序号是________. (写出所有正确结论的序号)

    说明:

    “正三角形沿轴滚动”包括沿轴正方向和沿轴负方向滚动. 沿轴正方向滚动指的是先以顶点为中心顺时针旋转, 当顶点落在轴上时, 再以顶点为中心顺时针旋转, 如此继续. 类似地, 正三角形可以沿轴负方向滚动.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设 为实数，且,

    (I)求方程的解；

    (II)若满足，求证：①②；

    (III)在（2）的条件下，求证：由关系式所得到的关于的方程存在，使

    查看答案和解析>>

    同步练习册答案