练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图放置的边长为2的正三角形沿轴滚动, 设顶点的纵坐标与横坐标的函数关系式是， 有下列结论:

    ①函数的值域是；②对任意的，都有；

    ③函数是偶函数；④函数单调递增区间为.

    其中正确结论的序号是________. (写出所有正确结论的序号)

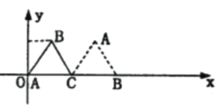
    说明:

    “正三角形沿轴滚动”包括沿轴正方向和沿轴负方向滚动. 沿轴正方向滚动指的是先以顶点为中心顺时针旋转, 当顶点落在轴上时, 再以顶点为中心顺时针旋转, 如此继续. 类似地, 正三角形可以沿轴负方向滚动.

    【答案】②③

    【解析】

    由已知中长为2的正三角形沿轴滚动，可画出滚动过程中点的轨迹，由图分别判断函数的奇偶性、单调性、周期性，可得到其值域，从而可得结论.

    点运动的轨迹如图所示. 由图可知：

    的值域为, ①错；

    是一个周期函数,周期为, ②正确；

    函数的图象关于轴对称，为偶函数, ③正确；

    函数的增区间为和, ④错，

    故答案为②③.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】以双曲线 （a＞0，b＞0）上一点M为圆心的圆与x轴恰相切于双曲线的一个焦点F，且与y轴交于P、Q两点．若△MPQ为锐角三角形，则该双曲线的离心率e的范围是（ ）
    A.
    B.（ ， ）
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知角α终边逆时针旋转 与单位圆交于点 ，且 ．
    （1）求 的值，
    （2）求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据条件，求下列曲线的方程．

    （1）已知两定点,曲线上的点到距离之差的绝对值为，求曲线的方程；

    （2）在 轴上的一个焦点与短轴两端点的连线互相垂直，且焦距为的椭圆的标准方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （1）当时，求的单调增区间.

    （2）若对任意的实数及任意的，不等式恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(1)求函数取得最大值时的自变量的集合并说出最大值；

    (2)求函数的单调递增区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）已知点为抛物线的焦点，点在抛物线上，且．

    （Ⅰ）求抛物线的方程；

    （Ⅱ）已知点，延长交抛物线于点，证明：以点为圆心且与直线相切的圆，必与直线相切．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线与轴交于，两点，点的坐标为，当变化时，解答下列问题：

    （）能否出现的情况?说明理由．

    （）证明过，，三点的圆在轴上截得的弦长为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为纪念重庆黑山谷晋升国家5A级景区五周年，特发行黑山谷纪念邮票，从2017年11月1日起开始上市．通过市场调查，得到该纪念邮票在一周内每1张的市场价y（单位：元）与上市时间x（单位：天）的数据如下：

    上市时间x天

    1

    2

    6

    市场价y元

    5

    2

    10

    （Ⅰ）分析上表数据，说明黑山谷纪念邮票的市场价y（单位：元）与上市时间x（单位：天）的变化关系，并判断y与x满足下列哪种函数关系，①一次函数；②二次函数；③对数函数，并求出函数的解析式；

    （Ⅱ）利用你选取的函数，求黑山谷纪念邮票市场价最低时的上市天数及最低的价格．

    查看答案和解析>>

    同步练习册答案