
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,当
,当![]() 变化时,解答下列问题:
变化时,解答下列问题:
(![]() )能否出现
)能否出现![]() 的情况?说明理由.
的情况?说明理由.
(![]() )证明过
)证明过![]() ,
,![]() ,
,![]() 三点的圆在
三点的圆在![]() 轴上截得的弦长为定值.
轴上截得的弦长为定值.
科目:高中数学 来源: 题型:
【题目】直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D. 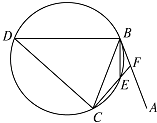
(1)证明:DB=DC;
(2)设圆的半径为1,BC=3,延长CE交AB于点F,求△BCF外接圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图放置的边长为2的正三角形![]() 沿
沿![]() 轴滚动, 设顶点
轴滚动, 设顶点![]() 的纵坐标与横坐标的函数关系式是
的纵坐标与横坐标的函数关系式是![]() , 有下列结论:
, 有下列结论:
①函数![]() 的值域是
的值域是![]() ;②对任意的
;②对任意的![]() ,都有
,都有![]() ;
;
③函数![]() 是偶函数;④函数
是偶函数;④函数![]() 单调递增区间为
单调递增区间为![]() .
.
其中正确结论的序号是________. (写出所有正确结论的序号)
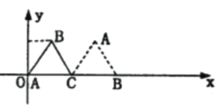
说明:
“正三角形![]() 沿
沿![]() 轴滚动”包括沿
轴滚动”包括沿![]() 轴正方向和沿
轴正方向和沿![]() 轴负方向滚动. 沿
轴负方向滚动. 沿![]() 轴正方向滚动指的是先以顶点
轴正方向滚动指的是先以顶点![]() 为中心顺时针旋转, 当顶点
为中心顺时针旋转, 当顶点![]() 落在
落在![]() 轴上时, 再以顶点
轴上时, 再以顶点![]() 为中心顺时针旋转, 如此继续. 类似地, 正三角形
为中心顺时针旋转, 如此继续. 类似地, 正三角形![]() 可以沿
可以沿![]() 轴负方向滚动.
轴负方向滚动.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)当![]() 时,若不等式
时,若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,若方程
时,若方程![]() 在
在![]() 上总有两个不等的实根, 求
上总有两个不等的实根, 求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
[20,30) | 30 | 18 |
[30,40) | 36 | 24 |
[40,50) | 12 | 9 |
[50,60] | 4 | 3 |
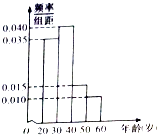
(1)若用分层抽样法从全校教师中抽取一个容量为40的样本,求从年龄段[20,30)抽取的人数;
(2)求全校教师的平均年龄;
(3)随机从年龄段[20,30)和[30,40)内各抽取1人,设这两人中两项培训结业考试成绩都优秀的人数为X,求X的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣![]() .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为![]() ,求实数a的值;
,求实数a的值;
(3)若f(x)<x2在(1,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com