
【题目】已知函数f(x)=lnx﹣![]() .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为![]() ,求实数a的值;
,求实数a的值;
(3)若f(x)<x2在(1,+∞)上恒成立,求实数a的取值范围.
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】试题分析:解 (1)由题意f(x)的定义域为(0,+∞),且f′(x)=![]() +
+![]() =
=![]() .因为a>0,所以f′(x)>0,故f(x)在(0,+∞)上是单调递增函数. 3分
.因为a>0,所以f′(x)>0,故f(x)在(0,+∞)上是单调递增函数. 3分
(2)由(1)可知,f′(x)=![]() .
.
①若a≥-1,则x+a≥0,即f′(x)≥0在[1,e]上恒成立,此时f(x)在[1,e]上为增函数,
所以f(x)min=f(1)=-a=![]() ,所以a=-
,所以a=-![]() (舍去). 5分
(舍去). 5分
②若a≤-e,则x+a≤0,即f′(x)≤0在[1,e]上恒成立,此时f(x)在[1,e]上为减函数,
所以f(x)min=f(e)=1-![]() =
=![]() a=-
a=-![]() (舍去). 7分
(舍去). 7分
③若-e<a<-1,令f′(x)=0得x=-a,当1<x<-a时,f′(x)<0,所以f(x)在[1,-a]上为减函数;当-a<x<e时,f′(x)>0,所以f(x)在[-a,e]上为增函数,所以f(x)min=f(-a)=ln(-a)+1=![]() a=-
a=-![]() .
.
综上所述,a=-![]() . 9分
. 9分
(3)因为f(x)<x2,所以lnx-![]() <x2.又x>0,所以a>xlnx-x3.
<x2.又x>0,所以a>xlnx-x3.
令g(x)=xlnx-x3,
h(x)=g′(x)=1+lnx-3x2,h′(x)=![]() -6x=
-6x=![]() . 11分
. 11分
因为x∈(1,+∞)时,h′(x)<0,h(x)在(1,+∞)上是减函数.
所以h(x)<h(1)=-2<0,即g′(x)<0,
所以g(x)在[1,+∞)上也是减函数,则g(x)<g(1)=-1,
所以a≥-1时,f(x)<x2在(1,+∞)上恒成立. 13分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,当
,当![]() 变化时,解答下列问题:
变化时,解答下列问题:
(![]() )能否出现
)能否出现![]() 的情况?说明理由.
的情况?说明理由.
(![]() )证明过
)证明过![]() ,
,![]() ,
,![]() 三点的圆在
三点的圆在![]() 轴上截得的弦长为定值.
轴上截得的弦长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为纪念重庆黑山谷晋升国家5A级景区五周年,特发行黑山谷纪念邮票,从2017年11月1日起开始上市.通过市场调查,得到该纪念邮票在一周内每1张的市场价y(单位:元)与上市时间x(单位:天)的数据如下:
上市时间x天 | 1 | 2 | 6 |
市场价y元 | 5 | 2 | 10 |
(Ⅰ)分析上表数据,说明黑山谷纪念邮票的市场价y(单位:元)与上市时间x(单位:天)的变化关系,并判断y与x满足下列哪种函数关系,①一次函数;②二次函数;③对数函数,并求出函数的解析式;
(Ⅱ)利用你选取的函数,求黑山谷纪念邮票市场价最低时的上市天数及最低的价格.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() ,且
,且![]() ,
,![]() )是定义在区间
)是定义在区间![]() 上的奇函数,
上的奇函数,
(1)求![]() 的值和实数
的值和实数![]() 的值;
的值;
(2)判断函数![]() 在区间
在区间![]() 上的单调性,并说明理由;
上的单调性,并说明理由;
(3)若![]() 且
且![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一隧道内设双行线路,其截面由一长方形和一抛物线构成。为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部(抛物线)在竖直方向上的高度之差至少为0.5m,若行车道总宽度AB为6m,请计算通过隧道的车辆的限制高度(精确度为0.1m)
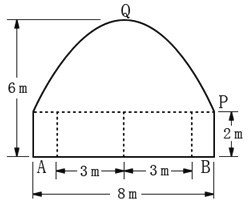
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍.
=1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍. 
(1)求椭圆C的方程;
(2)如图,直线l:y=kx+m与椭圆C相交于P,Q两点,若在椭圆C上存在点R,使OPRQ为平行四边形,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,椭圆
,椭圆![]() 上任意一点到椭圆两个焦点的距离之和为6.
上任意一点到椭圆两个焦点的距离之和为6.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]()
![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() (0,1),且
(0,1),且![]() =
=![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).

(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数![]() ,其中
,其中
![]() 是新样式单车的月产量(单位:件),利润
是新样式单车的月产量(单位:件),利润![]() 总收益
总收益![]() 总成本.
总成本.
(1)试将自行车厂的利润![]() 元表示为月产量
元表示为月产量![]() 的函数;
的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com