解:(I)据题意,f′(x)=3x
2+2bx+c≥0在(-∞,0]上恒成立,
且f′(x)=3x
2+2bx+c≤0在[0,1]上恒成立,
所以0是f(x)的极大值点,
所以f′(0)=0,
所以c=0
(II),由(I)知,f′(x)=3x
2+2bx=x(3x+2b),
当b>0时,由f′(x)<0解得
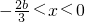
,
所以函数的递减区间为
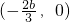
与在[0,1]上是减函数矛盾,不合题意.
当b<0时,由f′(x)<0解得
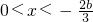
,
所以函数的递减区间为
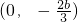
,
因为函数在[0,1]上是减函数,
所以f′(x)≤0在[0,1]上恒成立,
所以

解得b
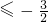
(III)
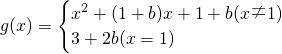
当x≠1时,b≠-3时,
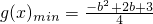
,
因为
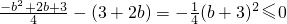
,
所以x∈R时,h(b)=
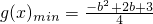
,
又b
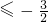
,b≠-3时,h(b)是关于b的增函数,
所以
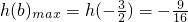
分析:(I)据题意,所以0是f(x)的极大值点,判断出0是f(x)的极大值点,得到f′(0)=0,求出c=0;
(II),当b>0时,由f′(x)<0得到函数的递减区间为
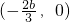
与在[0,1]上是减函数矛盾,不合题意.当b<0时,由f′(x)<0得到函数的递减区间为
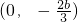
,令

得b的范围.
(III)求出g(x)的解析式,分段求出各段函数的最小值,比较出最小值h(b),利用二次函数的性质求出h(b)的最大值.
点评:本题考查函数在极值点处的导数值为0,函数递增时,导函数大于等于0;考查分段函数的最值应该分段来求,属于较难的题.

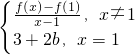 ,若g(x)的最小值为h(b),求h(b)的最大值.
,若g(x)的最小值为h(b),求h(b)的最大值.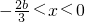 ,
,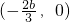 与在[0,1]上是减函数矛盾,不合题意.
与在[0,1]上是减函数矛盾,不合题意.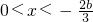 ,
,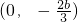 ,
, 解得b
解得b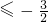
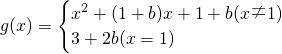
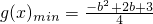 ,
,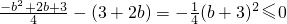 ,
,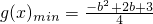 ,
,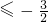 ,b≠-3时,h(b)是关于b的增函数,
,b≠-3时,h(b)是关于b的增函数,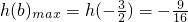
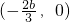 与在[0,1]上是减函数矛盾,不合题意.当b<0时,由f′(x)<0得到函数的递减区间为
与在[0,1]上是减函数矛盾,不合题意.当b<0时,由f′(x)<0得到函数的递减区间为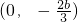 ,令
,令 得b的范围.
得b的范围.

 阅读快车系列答案
阅读快车系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<