
 -
-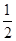 alnx,a∈R.
alnx,a∈R.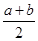 )≤
)≤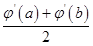 ≤φ′(
≤φ′(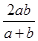 ).
).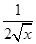 -
-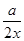 =
=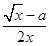 (x>0).
(x>0).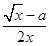 >0,f(x)在(0,+∞)上是增函数,无最小值.
>0,f(x)在(0,+∞)上是增函数,无最小值.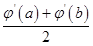 =-
=-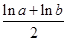 =-ln
=-ln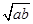 , ①
, ①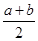 )=-ln(
)=-ln(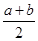 )≤-ln
)≤-ln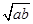 , ②
, ②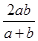 )=-ln(
)=-ln(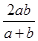 )≥-ln
)≥-ln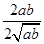 =-ln
=-ln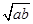 , ③
, ③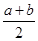 )≤
)≤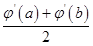 ≤φ′(
≤φ′(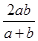 ). 14分
). 14分

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源:不详 题型:解答题
 ,
, 的图象经过
的图象经过 和
和 两点,如图所示,且函数
两点,如图所示,且函数 的值域为
的值域为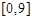 .过该函数图象上的动点
.过该函数图象上的动点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
,连接 .
.
 的解析式;
的解析式; 的面积为
的面积为 ,求
,求 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (
( 是自然对数的底数).
是自然对数的底数). 在
在 处的切线也是抛物线
处的切线也是抛物线 的切线,求
的切线,求 的值;
的值; 时,是否存在
时,是否存在 ,使曲线
,使曲线 在点
在点 处的切线斜率与
处的切线斜率与 在
在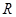 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是实数,函数
是实数,函数 ,
, 和
和 ,分别是
,分别是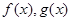 的导函数,若
的导函数,若 在区间
在区间 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间 上单调性一致.
上单调性一致. ,若函数
,若函数 和
和 在区间
在区间 上单调性一致,求实数
上单调性一致,求实数 的取值范围;
的取值范围; 且
且 ,若函数
,若函数 和
和 在以
在以 为端点的开区间上单调性一致,求
为端点的开区间上单调性一致,求 的最大值.
的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com