
【题目】已知数列{an}为等差数列,a1=3且(a3﹣1)是(a2﹣1)与a4的等比中项.
(1)求an;
(2)若数列{an}的前n项和为Sn , bn= ![]() ,Tn=﹣b1+b2+b3+…+(﹣1)nbn , 求Tn .
,Tn=﹣b1+b2+b3+…+(﹣1)nbn , 求Tn .
【答案】
(1)解:设等差数列{an}的公差为d,a1=3且(a3﹣1)是(a2﹣1)与a4的等比中项.
∴(3+2d﹣1)2=(3+3d)(3+d﹣1),整理为:d2﹣d﹣2=0,解得d=2,或﹣1(舍去).
∴an=2n+1.
(2)解:Sn= ![]() =n2+2n
=n2+2n
bn= ![]() =
= ![]() =
= ![]() ,
,
当n为偶数时,Tn=﹣b1+b2+b3+…+(﹣1)nbn=﹣ ![]() +
+ ![]() ﹣…+
﹣…+ ![]() =﹣1+
=﹣1+ ![]() =
= ![]() .
.
当n为奇数时,Tn=﹣b1+b2+b3+…+(﹣1)nbn=﹣ ![]() +
+ ![]() ﹣…﹣
﹣…﹣ ![]() =﹣1﹣
=﹣1﹣ ![]() =
= ![]() .
.
∴Tn= 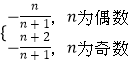
【解析】(1)设等差数列{an}的公差为d,a1=3且(a3﹣1)是(a2﹣1)与a4的等比中项.可得(3+2d﹣1)2=(3+3d)(3+d﹣1),整理为:d2﹣d﹣2=0,解得d并且验证即可得出.(2)Sn= ![]() =n2+2n,bn=
=n2+2n,bn= ![]() =
= ![]() =
= ![]() ,对n分类讨论即可得出.
,对n分类讨论即可得出.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系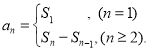 .
.


科目:高中数学 来源: 题型:
【题目】知函数f(x)=ax2﹣2x+lnx(a≠0,a∈R).
(1)判断函数 f (x)的单调性;
(2)若函数 f (x)有两个极值点x1 , x2 , 求证:f(x1)+f(x2)<﹣3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA. 
(1)求证:BE⊥平面PAC;
(2)求直线AB与平面BEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行. (Ⅰ)求A;
=(cosA,sinB)平行. (Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有四个函数:①y=xsinx;②y=xcosx;③y=x|cosx|;④y=x2x的图象(部分)如图: 
则按照从左到右图象对应的函数序号安排正确的一组是( )
A.①④③②
B.③④②①
C.④①②③
D.①④②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若命题p:从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一;命题q:在边长为4的正方形ABCD内任取一点M,则∠AMB>90°的概率为 ![]() ,则下列命题是真命题的是( )
,则下列命题是真命题的是( )
A.p∧q
B.(p)∧q
C.p∧(q)
D.q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年春晚过后,为了研究演员上春晚次数与受关注度的关系,某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计,得到如下数据:
上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
粉丝数量y(单位:万人) | 10 | 20 | 40 | 80 | 100 |
(1)若该演员的粉丝数量g(x)≤g(1)=0与上春晚次数x满足线性回归方程,试求回归方程 ![]() =
= ![]() x+
x+ ![]() ,并就此分析,该演员上春晚12次时的粉丝数量;
,并就此分析,该演员上春晚12次时的粉丝数量;
(2)若用 ![]() (i=1,2,3,4,5)表示统计数据时粉丝的“即时均值”(四舍五入,精确到整数),从这5个“即时均值”中任选2数,记所选的2数之和为随机变量η,求η的分布列与数学期望. 参考公式:
(i=1,2,3,4,5)表示统计数据时粉丝的“即时均值”(四舍五入,精确到整数),从这5个“即时均值”中任选2数,记所选的2数之和为随机变量η,求η的分布列与数学期望. 参考公式: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=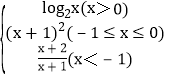 ,若对任意给定的m∈(1,+∞),都存在唯一的x0∈R满足f(f(x0))=2a2m2+am,则正实数a的取值范围为( )
,若对任意给定的m∈(1,+∞),都存在唯一的x0∈R满足f(f(x0))=2a2m2+am,则正实数a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对一切实数x、y,不等式 ![]() ﹣cos2x≥asinx﹣
﹣cos2x≥asinx﹣ ![]() 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.(﹣∞, ![]() ]
]
B.[3,+∞)
C.[﹣2 ![]() ,2
,2 ![]() ]
]
D.[﹣3,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com