
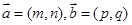 ,令
,令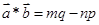 。给出以下四个命题:(1)若
。给出以下四个命题:(1)若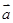 与
与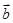 共线,则
共线,则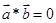 ;(2)
;(2)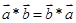 ;(3)对任意的
;(3)对任意的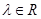 ,有
,有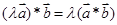 ;(4)
;(4)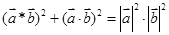 。
。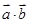 指
指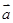 与
与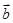 的数量积)
的数量积)| A.(1)(2)(3) | B.(2)(3)(4) | C.(1)(3)(4) | D.(1)(2)(4) |
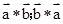 判断出(2)假;利用对“*”的定义求出
判断出(2)假;利用对“*”的定义求出
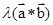

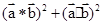 判断出(4)对;综合可得答案.
判断出(4)对;综合可得答案.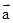 ∥
∥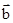 ,则mq-np=0,所以
,则mq-np=0,所以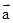 *
*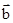 =0,故(1)真
=0,故(1)真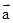 *
*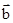 =mq-np;
=mq-np;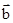 *
*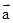 =pn-qm,∴
=pn-qm,∴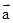 *
*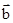 ≠
≠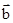 *
*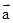 故(2)假
故(2)假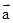 )*
)*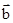 =(λm,λ n)*(p,q)=λmq-λnp;λ(
=(λm,λ n)*(p,q)=λmq-λnp;λ(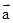 *
*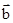 )=λ(mq-np)=λmq-λnp
)=λ(mq-np)=λmq-λnp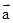 )*
)*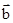 =λ(
=λ(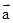 *
*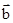 )故(3)真
)故(3)真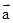 *
*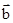 )2+(
)2+(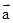 ?
?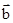 )2=(mq-np)2 +(mp+nq)2=(m2+n2)(p2+q2)=|
)2=(mq-np)2 +(mp+nq)2=(m2+n2)(p2+q2)=|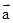 |2?|
|2?|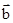 |2,故(4)真
|2,故(4)真

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com