
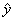 =bx+a必过( )
=bx+a必过( )| A.(0,0)点 | B.(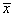 ,0)点 ,0)点 | C.(0,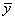 )点 )点 | D.(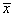 , ,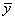 )点 )点 |
科目:高中数学 来源:不详 题型:单选题
| A.500人 | B.1000人 | C.1500人 | D.2000人 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 月收入(元) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) | [6000,7000) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 反对人数 | 4 | 8 | 12 | 5 | 2 | 1 |
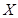 ,求
,求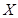 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
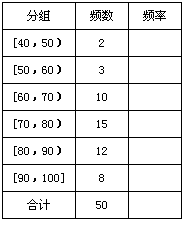
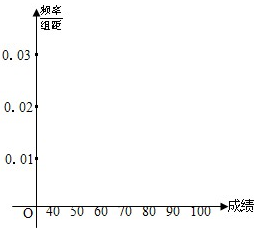
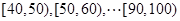 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.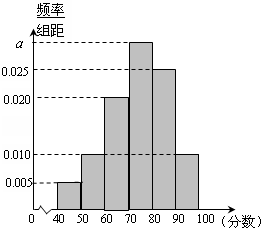
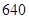 人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
人,试估计该校高一年级期中考试数学成绩不低于60分的人数;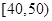 与
与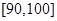 两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率。
两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.① | B.②③ | C.①③ | D.①②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

A.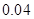 | B.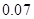 | C.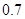 | D.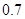 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com