
已知椭圆C1的中心在坐标原点,两个焦点分别为F1(-2,0),F2(2,0),点A(2,3)在椭圆C1上,过点A的直线L与抛物线C2:x2=4y交于B,C两点,抛物线C2在点B,C处的切线分别为l1,l2,且l1与l2交于点P.
(1)求椭圆C1的方程;
(2)是否存在满足|PF1|+|PF2|=|AF1|+|AF2|的点P?若存在,指出这样的点P有几个(不必求出点P的坐标);若不存在,说明理由.
解:(1)设椭圆方程为 +
+ =1(a>b>0),
=1(a>b>0),
由题意可知2a=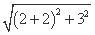 +
+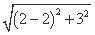 =8.
=8.
∴a=4,b2=a2-c2=12.
∴椭圆方程为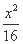 +
+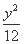 =1.
=1.
(2)设B(x1,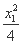 ),C(x2,
),C(x2,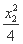 ),
),
直线BC的斜率为k,则k=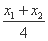 .
.
由y=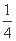 x2,得y′=
x2,得y′= x.
x.
∴点B、C处的切线l1、l2的斜率分别为 x1,
x1, x2,
x2,
∴l1的方程为y-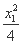 =
= x1(x-x1),
x1(x-x1),
即y= x1x-
x1x-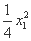 ,
,
同理,l2的方程为y= x2x-
x2x-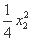 .
.
由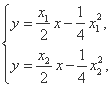
解得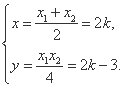
∴P(2k,2k-3).
∵|PF1|+|PF2|=|AF1|+|AF2|,
∴点P在椭圆C1: 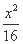 +
+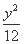 =1上,
=1上,
∴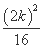 +
+ =1.
=1.
化简得7k2-12k-3=0.(*)
由Δ=122-4×7×(-3)=228>0,
可得方程(*)有两个不等的实数根.
∴满足条件的点P有两个.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
已知椭圆C:  +
+ =1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF=
=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF= ,则C的离心率为( )
,则C的离心率为( )
(A)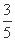 (B)
(B)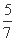 (C)
(C) (D)
(D)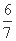
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C1:  +
+ =1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
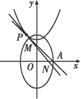
(1)求椭圆C1的方程;
(2)设点P在抛物线C2:y=x2+h(h∈R)上,C2在点P处的切线与C1交于点M,N.当线段AP的中点与MN的中点的横坐标相等时,求h的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
某校要从高一、高二、高三共2 012名学生中选取50名组成志愿团,若采用下面的方法选取,先用简单随机抽样的方法从2 012人中剔除12人,剩下的2 000人再按分层抽样的方法进行,则每人入选的概率( )
A.都相等且为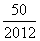 B.都相等且为
B.都相等且为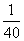
C.不会相等 D.均不相等
查看答案和解析>>
科目:高中数学 来源: 题型:
某单位有2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如下表所示:
| 人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
| 老年 | 40 | 40 | 40 | 80 | 200 |
| 中年 | 80 | 120 | 160 | 240 | 600 |
| 青年 | 40 | 160 | 280 | 720 | 1 200 |
| 小计 | 160 | 320 | 480 | 1 040 | 2 000 |
(1)若要抽取40人调查身体状况,则应怎样抽样?
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?
(3)若要抽20人调查对2016年巴黎奥运会筹备情况的了解,则应怎样抽样?
查看答案和解析>>
科目:高中数学 来源: 题型:
设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( )
A.x和y正相关
B.x和y的相关系数为直线l的斜率
C.x和y的相关系数在-1到0之间
D.当n为偶数时,分布在l两侧的样本点的个数一定相同

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com