练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中， a、b、c分别是角A、B、C的对边，△ABC的周长为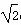＋2，且sinA＋sinB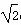＝sinC.

    (1) 求边c的长；

    (2) 若△ABC的面积为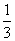sinC，求角C的度数．


    解：(1) 在△ABC中， ∵ sinA＋sinB＝sinC，由正弦定理，得a＋b＝c ，∴ a＋b＋c＝c＋c＝(＋1)c＝＋2.

    ∴ a＋b＝2，c＝.

    (2) 在△ABC中， S△ABC＝absinC＝sinC，

    ∴ ab＝ ，即ab＝.

    又a＋b＝2，在△ABC中，由余弦定理，得cosC＝＝，又在△ABC中∠C∈(0，π)，

    ∴ ∠C＝60°.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设数列{an}的前n项和为Sn.已知a1＝1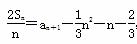，，n∈N*.

    (1) 求a2的值；

    (2) 求数列{an}的通项公式；

    (3) 证明：对一切正整数n，有<.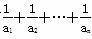

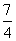    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在海岸A处，发现北偏西75°的方向，距离A 2海里的B处有一艘走私船，在A处北偏东45°方向，距离A (－1)海里的C处的缉私船奉命以10海里/小时的速度追截走私船．此时，走私船正以10海里/小时的速度从B向北偏西30°方向逃窜，问缉私船沿什么方向能最快追上走私船？

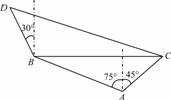
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝Asin，x∈R，A>0，0<φ<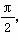，y＝f(x)的部分图象如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为(1，A)．

    (1) 求f(x)的最小正周期及φ的值；

    (2) 若点R的坐标为(1，0)，∠PRQ＝，求A的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝cos的最小正周期为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若sin(＋θ)＝，则cos2θ＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知α、β∈(0，π)，且tan(α－β)＝，tanβ＝－，求2α－β的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABC中，内角A、B、C的对边分别为a、b、c，且，求角C的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知cosα＝，cos(α－β)＝，且0＜β＜α＜，求β.

    查看答案和解析>>

    同步练习册答案